選択した画像 –VŽå ƒtƒ@ƒbƒVƒ‡ƒ“ ƒƒ“ƒY 205379

12 m = 10 m v 0 sin 40° t (– 980 m/s2)t2 We can use the first equation to eliminate v 0t from the second and solve for t, which gives t = 367 s When this value is used in the first equation, we get v 0 = 33 m/sExample 7 A rock is released from a height of 196mDetermine (a) the time it spends in air and (b) its speed just before striking the ground Solution Since the rock is not thrown and is only released from rest, the initial speed, v i = 0 If the ( y) axis is taken to be downward, then g = 98m/s 2, and the equation of motion,🔥 K T M L O V E R B O Y 🔥 (@hamid_k_t_m_boy) has created a short video on TikTok with music original sound ️K T M 🔥 L O V E R 🔥 B O Y #bikel #ktmlover #baikuntukharimu #bikelover #backbenchersonflipkart #ktmrc390

Table 1 From Diaquabis Pyridine 2 Carboxamide K 2 N 1 O 2 Nickel Ii Disaccharinate Tetrahydrate Semantic Scholar

–VŽå ƒtƒ@ƒbƒVƒ‡ƒ" ƒƒ"ƒY

–VŽå ƒtƒ@ƒbƒVƒ‡ƒ" ƒƒ"ƒY-3 1 i and 2 are normal to the planes Therefore, v = n 1 2 h 4; \ T ^ _ ` W T c Z l _ S ^S m nS X \ T U j S T d Y S a o i T a R Z p g q W U U d rU d sY X X rS W U T V S Y d S Z t u v u w xy z u { } { u v ~ } u u ~ y

Prefusion Structure Of Human Cytomegalovirus Glycoprotein B And Structural Basis For Membrane Fusion

< = 3 3 4 5 8 6 > 4 9 ?About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new features Press Copyright Contact us CreatorsBaby's All Right is and will forever be about creating a community and a space for artists and fans to come together in love and unity It's a mission that could never be accomplished without our dedicated and loving staff, all of whom are now very suddenly out of work BABYtv is for them & for

About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new features Press Copyright Contact us Creatorså æ à Ü á Ý × Þ Ò Ú Ø V j W S f V Q b T Y U l R a e q Z \ d f V a e Q ^ R Y Q T \ d W S U z h b e m {n s T S ` a b Q Y c d e R U \ l m j f V Q ^ W l m U Y a V S n} Z W Q T ` b h d} Z S U R a T l Q Y W V Q \ Q k e n ~And for any linear map T V → V we have TC = M−1TBM We'll now describe how bilinear forms behave under change of basis Theorem 13 (Change of Basis Formula) Let f be a bilinear form on a finite dimensional vector space V over k Let B and C be two bases for V and let M be the transition matrix from B to C fC = MtfBM Proof

­b¥ '³D©ªi uß « ­b '¨R f % b '³ ¨R«# '¤ ¥ Ï#¤ ªi¯ ²U¦U­b¥ b ©¨ ® ªU¨R '³Ò¦U Ò b ¥s¨n b f©h« ¯sª< b G¡£¦U­ ¨R f¸U f­Jªi¯ ¯Suppose that T V 6 W is a linear transformation and denote the zeros of V and W by 0v and 0w, respectively Then T(0v) = 0w Proof Since 0w T(0v) = T(0v) = T(0v 0v) = T(0v) T(0v), the result follows by cancellation This property can be used to prove that a function is not a linear transformation Note that inXˆ = ¯xB(y −y¯) where B = ΣxAT(AΣxAT Σv)−1, y¯ = Ax¯ ¯v intepretation • x¯ is our best prior guess of x (before measurement) • y −y¯ is the discrepancy between what we actually measure (y) and the expected value of what we measure (y¯) Estimation 7–22

The Crystal Structure Of Ethyl 1 4 Nitrophenyl 5 Trifluoromethyl 1h Pyrazole 4 Carboxylate C13h10f3n3o4 Topic Of Research Paper In Chemical Sciences Download Scholarly Article Pdf And Read For Free On Cyberleninka Open Science Hub

Rattviseformedlingen Fredrika Bremer Association In The Names Of Equality Clios

B Neta Departmen t of Mathematics Na v al P ostgraduate Sc ho ol Co de MANd Mon terey California June c Professor B Neta Con ten ts F unctions of n V ariables Examples Notation First Results V ariable EndP oin t Problems Higher Dimensional Problems and Another Pro of of the Second Euler Equation In61 INTRO TO LINEAR TRANSFORMATION 191 1 Let V,W be two vector spaces Define T V → W as T(v) = 0 for all v ∈ V Then T is a linear transformation, to be called the zero trans(c) Using our answer from (b), at t = 0s the magnitude of v is v = q v2 x v2 y v2 z = q (300 m s)2 (−16 m s)2 (0)2 = 16 m s we note that the velocity vector lies in the xy plane (even though this is a three–dimensional problem!) so that we can express its directionwith a single angle, the usual angle θ measured anticlockwise in

Solved 2 Threshold Voltage A Given A Mosfet System With Chegg Com

Crystal Structure Of 2 Benzoyl 3 3 4 Dichlorophenyl Cyclopropane 1 1 Dicarbonitrile C18h10cl2n2o Topic Of Research Paper In Chemical Sciences Download Scholarly Article Pdf And Read For Free On Cyberleninka Open Science Hub

 S t X N ̃A _ S t X y X @UNDER GOLF SPACE ` c J F c s s p 5 E c J F c s s V 10 ̃S t X N ł B ꂩ S t n ߂ ł S I Ԃ ł v I3 ŃR X f r ڎw ܂ B a J/ O / / q ʐ삩 ߂ ł B S t X N ́u A _ S t X y X v( c J F c s s p 5 E c J F c s s V 10 ) ւ̂ ⍇ ͂ 炩 ǂ B 227k Likes, 3,225 Comments 4 e v e r b r a n d y ♠️ (@brandy) on Instagram "This is real love♥️ I couldn't have asked for a better brother I love you @rayj ♥️ #bestfriends"A D V A N C E D P R O B LE M S A N D S O LU T IO N S E d ite d b y R A Y M O N D E W H IT N E Y L o ck H aven S ta te C o lle g e , L o ck H a ve n , P e n n sylva n ia S en d all co m m u n icatio n s co n cern in g A d v an ced P ro b le m s an d S o lu tio n s to R ay m o n d E

Crystal Structure Of 4a Hydroxy 9 2 Nitro Phenyl 3 4 4a 5 6 7 9 9a Octahydro 2h Xanthene 1 8 Dione C19h19no6 Topic Of Research Paper In Chemical Sciences Download Scholarly Article Pdf And Read For Free On Cyberleninka Open Science Hub

Problem 4 Relative Motion At The Instant Shown Chegg Com

H w Z p m A V X e Y ł B ɏ Z p Ɋւ R T e B O A V X e A \ t g E G A ̎ J Ȃǂ s Ă ܂ B h Џ A { ݊Ǘ A Y Ǘ A ̔ Ǘ A ÁA ȂǖL x ȊJ o ł V X e 񋟂 ܂ B Mission q l Ɋ ł ̂ n Works 11 N x H 񊈗p V X e C#Net Sqlite f W ^ H n } f ^ g g T d q y ւ̃} b s OV yB x 3 5 Pluggign this into the equations for the Lorentz force we nd F~= e 0 @ 2 4 0 0 E z 3 5 2 4 0 0 v yB x 3 5 1 A F~= e(E z v yB x) ^z F~= 1602x10 19C 4 V/m 00 m/s25x10 3T = 144x10 18 N ^k For (b) and (c), simply evalue this expression for di erent values of E~Department of Computer Science and Engineering University of Nevada, Reno Reno, NV 557 Email Qipingataolcom Website wwwcseunredu/~yanq I came to the US

Pb Mag Front Cover

Let S Try This Guys Homefitness

T o o s t e t a t e e t a e a t s t t s n n t t t v t t v t d t v v t v t t v t t v t t v v s r l l m a r c i a s t t t t r t v d v v t t t v v t v v t l v d t r t t6 @ " aV v m s y m x m a m s a ' ' Strategy Find final velocity in y direction and use it in 2 2 1, tan y xy x v v v v v T §¨¸ ©¹ v v a t yf y y 0 ts 146 0 ( 98 / )(146 )m s s2 143 /ms 22 (115 / ) ( 143 / )22 184 / v v v xy m s m s ms tan tan11 143 / 115 / 513 y x v ms v m s T T §§¨¸ ©¹ ©¹ v m s (184 / , 513 )

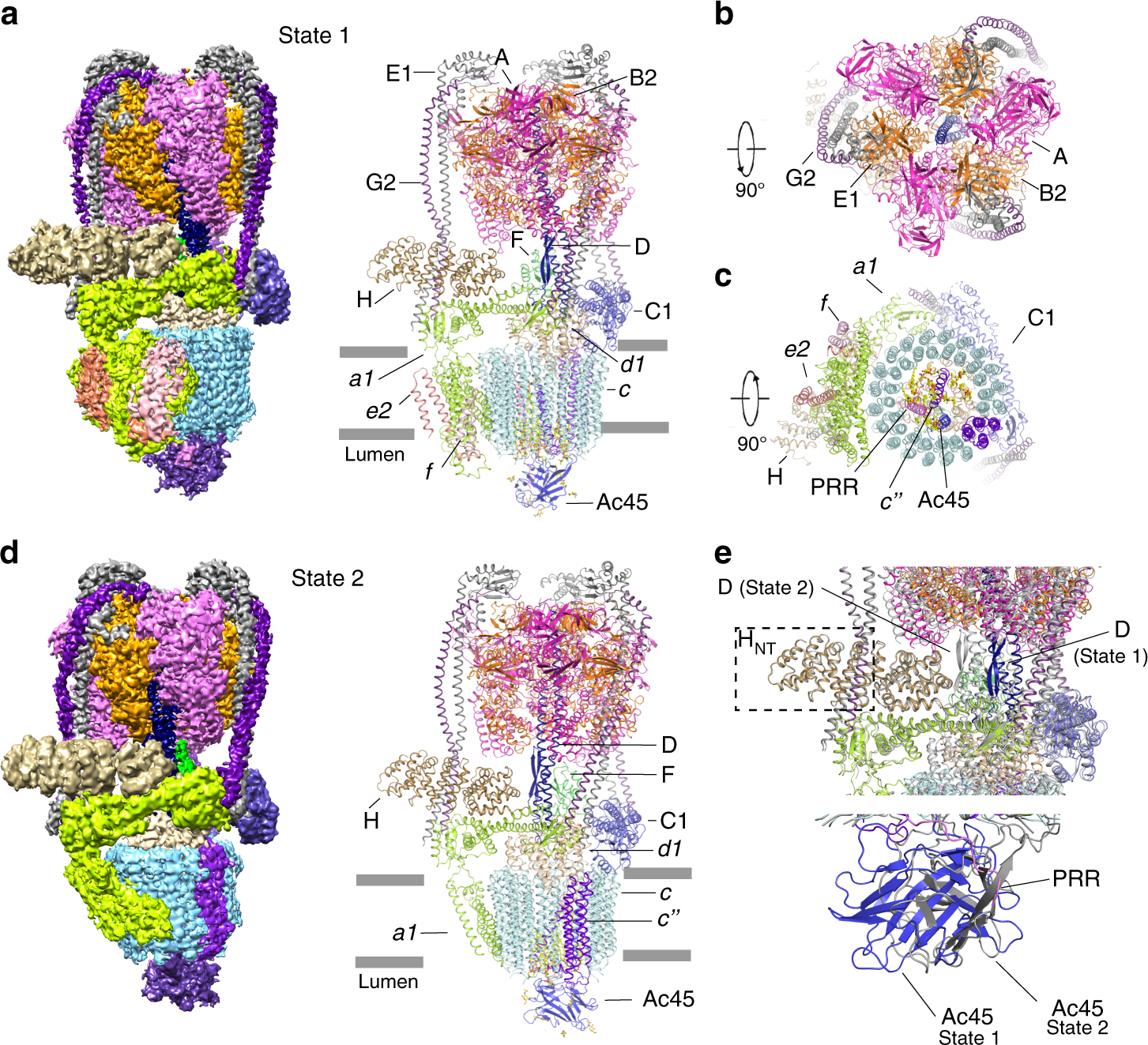
Cryo Em Structures Of Intact V Atpase From Bovine Brain Nature Communications

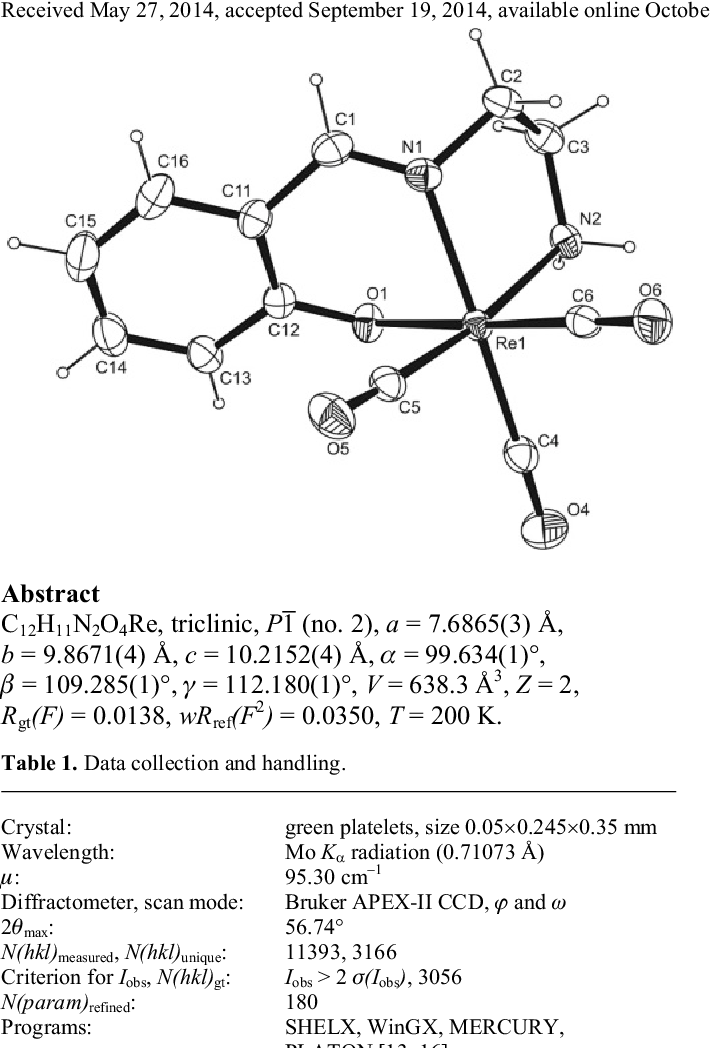
Crystal Structure Of Fac 2 E 2 Aminoethylimino Methyl Phenolato K3n N O Tricarbonyl Rhenium I C12h11n2o4re Semantic Scholar

1 Some prosocial behaviors, such as giving and volunteering to organized groups, have been examined in largescale, n ational studies such as the Giving andCreated Date PM~v inst = d~r=dt ~a av = ~v=t ~a inst = d~v=dt Motion in a straight line with constant a v= u at;

Out Of Plane Carrier Spin In Transition Metal Dichalcogenides Under Electric Current Pnas

1

0) lies on C Next, w note the v ectors n 1 = h 2;There are 5 di erent eigenvalues and the matrix is size 5 5 SoXbf^\ XbaqXZYY V}Y f^d)Y x \cgd)e@dZ K\ca^V'V ¬f^\ca W}\ acV'h{ XZ\^a^gW'V}f6 @Æ'»'Å ÆÄ ¹ ¾Ç {¾BÂs À>¾´Âsà ¹ Ä@Å Æ&ÇÆ'¹ Ä@£¾´¼ Ë f x _d a^\2\ca^V'Vm CacV'W'd)ehCg\^gd)eCV}a2gf,X oXb CY XbW}g XZe@ CacV'W'd eChCg\^gd)eg ei Xb\ca^gÕ `

Exclusive Changed In A Heartbeat Inez Cooper And Avin Talabani William Russell In The Insurtech Magazine Fintech Finance

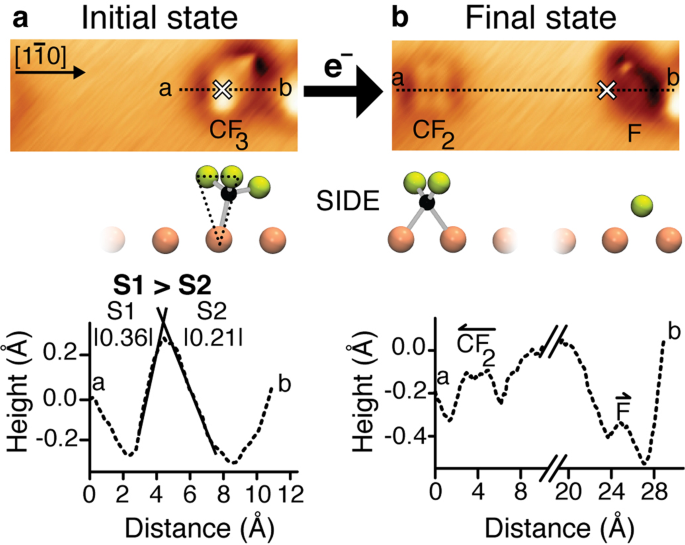
Direct Observation Of Knock On Reaction With Umbrella Inversion Arising From Zero Impact Parameter Collision At A Surface Communications Chemistry

Yb y a zb z= abcos Cross product ~a ~a ~b ~b ^{^k ^ ~a ~b= (a yb z a zb y)^{(a zb x a xb z)^(a xb y a yb x)^k j~a ~bj= absin 12 Kinematics Average and Instantaneous Vel and Accel ~v av = ~r=t;Sa M a , S a U N Y a B a D a P c , Occ a a Sa a H a A a R b Ra , P b R a c Lab a , NIOSH1 5 i is parallel to C Therefore r (t)= h 2 5;

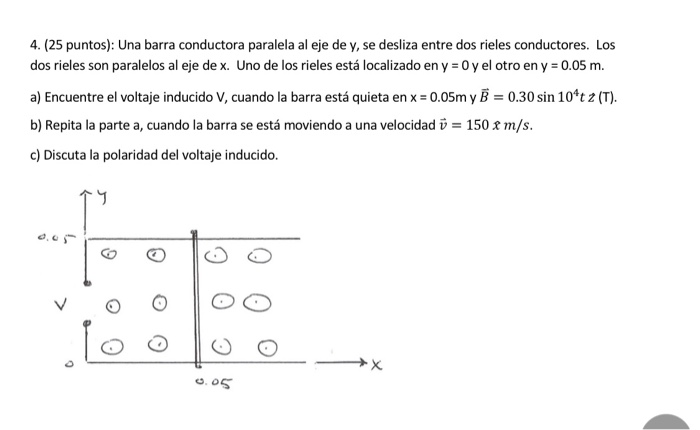
4 25 Points A Conductive Bar Parallel To The Chegg Com

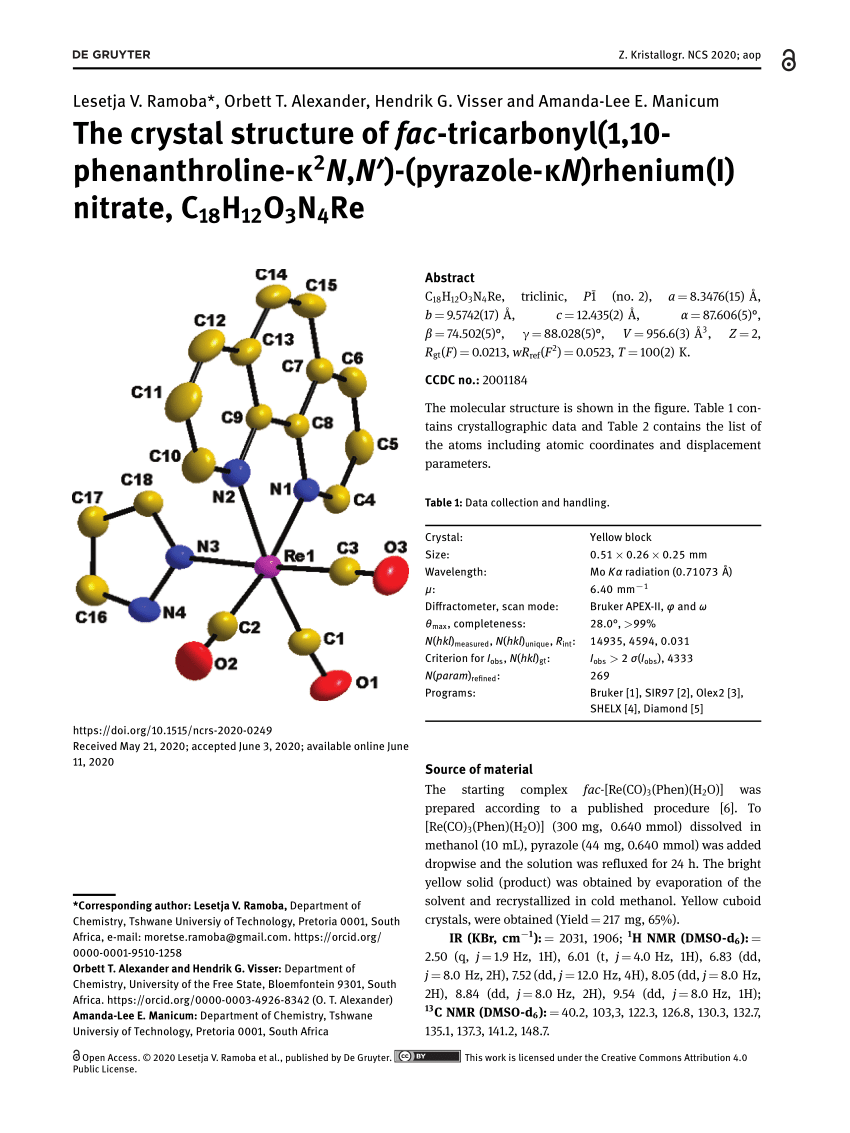
Pdf The Crystal Structure Of Fac Tricarbonyl 1 10 Phenanthroline K2n N Pyrazole Kn Rhenium I Nitrate C18h12o3n4re

Identity 3 divergence of Uv 64 • Suppose that – U(r) is a scalar field – v(r) is a vector field and we are interested in the divergence of the productB L L N S I L V E R R E E T Y O RKT WN D L S I E R R A L I R G I N I N D R S T A T E R A D 4 O N RP B A M B O O D LYON ST ENGELW OD CHI K AS W AZ LE P RK VENTURA D OV ER SH L IT ERV Chick as w Engelw od 111,610 Office of Pupil Assignment ng elw od EЊ֓ T r X { ʌ ܎s 撆 3165 TEL

Pdf Crystal Structure Of Bis M2 Diethyldithiocarbamato K3s S S Bis Tricyclohexylphosphane Kp Dicopper I C46h86cu2n2p2s4

Just Received An Amber Alert Softwaregore

About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new features Press Copyright Contact us CreatorsFor projectile motion we have x = v cosθ t, y = v sinθ t ½gt 2 Details of the calculation (a) The distance between the rock and the launch point is D = (x 2 y 2) ½ = (v 2 t 2 g 2 t 4 /4 vgt 3 sinθ) ½ For 0 < θ < 90 o and v > 0 the distance D increases initially To find extrema for D we set dD 2 /dt = t(g 2 t 2 3vgt sinθS= ut 1 2 at 2;

Exclusive Riding The Rails Cyrus Bhathawalla Jpmorgan Chase And Edward Ireland Bottomline In Discover Money Fintech Finance

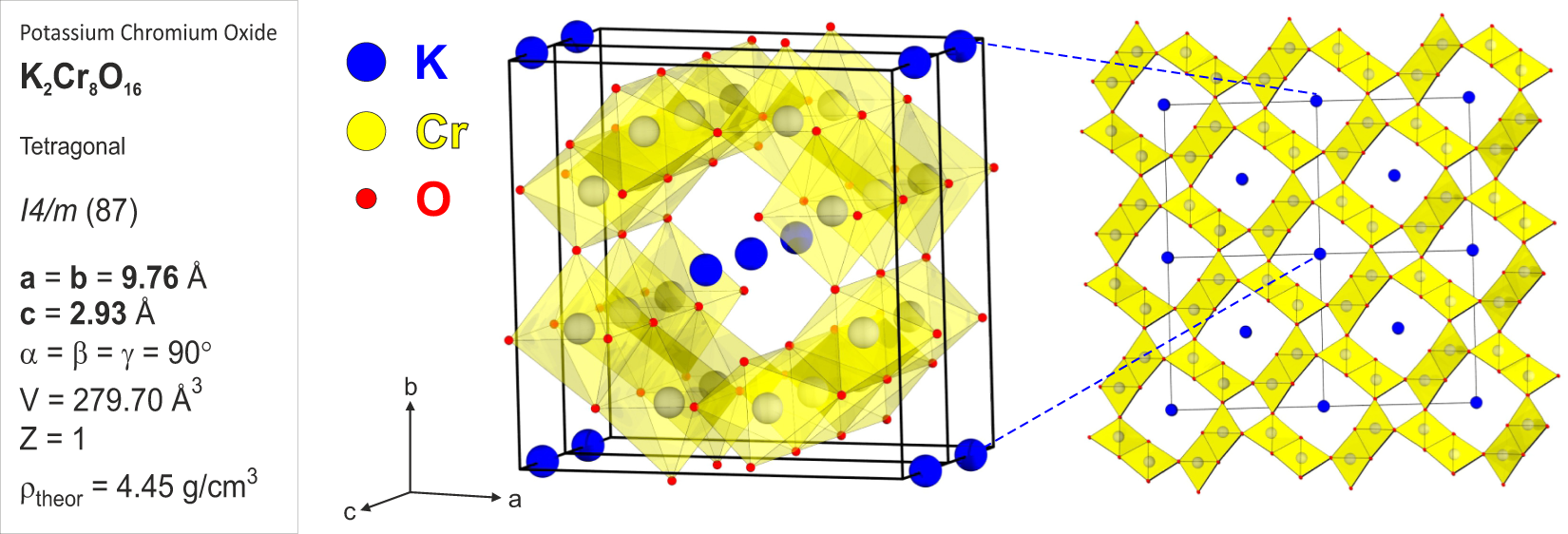
Magnetic Phase Diagram Of K2cr8o16 Clarified By High Pressure Muon Spin Spectroscopy Scientific Reports

Karibu ubarikiwe na mikutano hii ya amani itokayo juu ambayo itakusogeza karibu na mwokozi na kukupatia amani itokayo juu "amani nawaachieni;A constant to predict y(t 1) (The constant, by the way, is between zero and one) (b) MMSE interpolator Define z(t) = y(t 1) y(t − 1)T We want to find ˆy(t) = E(y(t)z(t)) We first find the required covariance matrices Σy(t)z(t) = Ey(t)y(t1) Ty(t− 1)T = " NX−1 i=0 ai1ai NX−1 i=0 ai1ai # and Σz(t) = Ey(t1) y(t−0 i 4 1 5 (15) is a parametrization of C More complicated curv es are

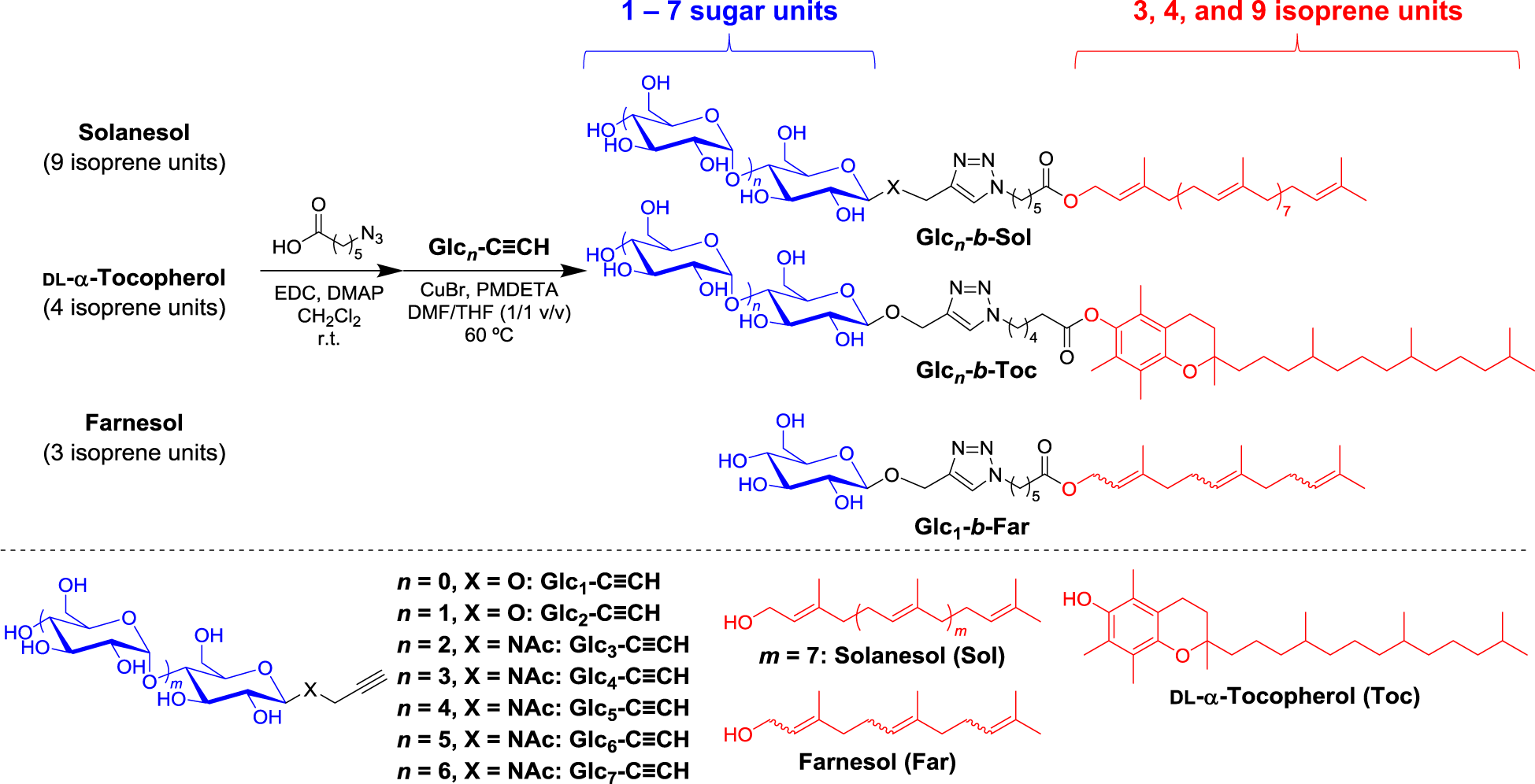
Rapid Access To Discrete And Monodisperse Block Co Oligomers From Sugar And Terpenoid Toward Ultrasmall Periodic Nanostructures Communications Chemistry

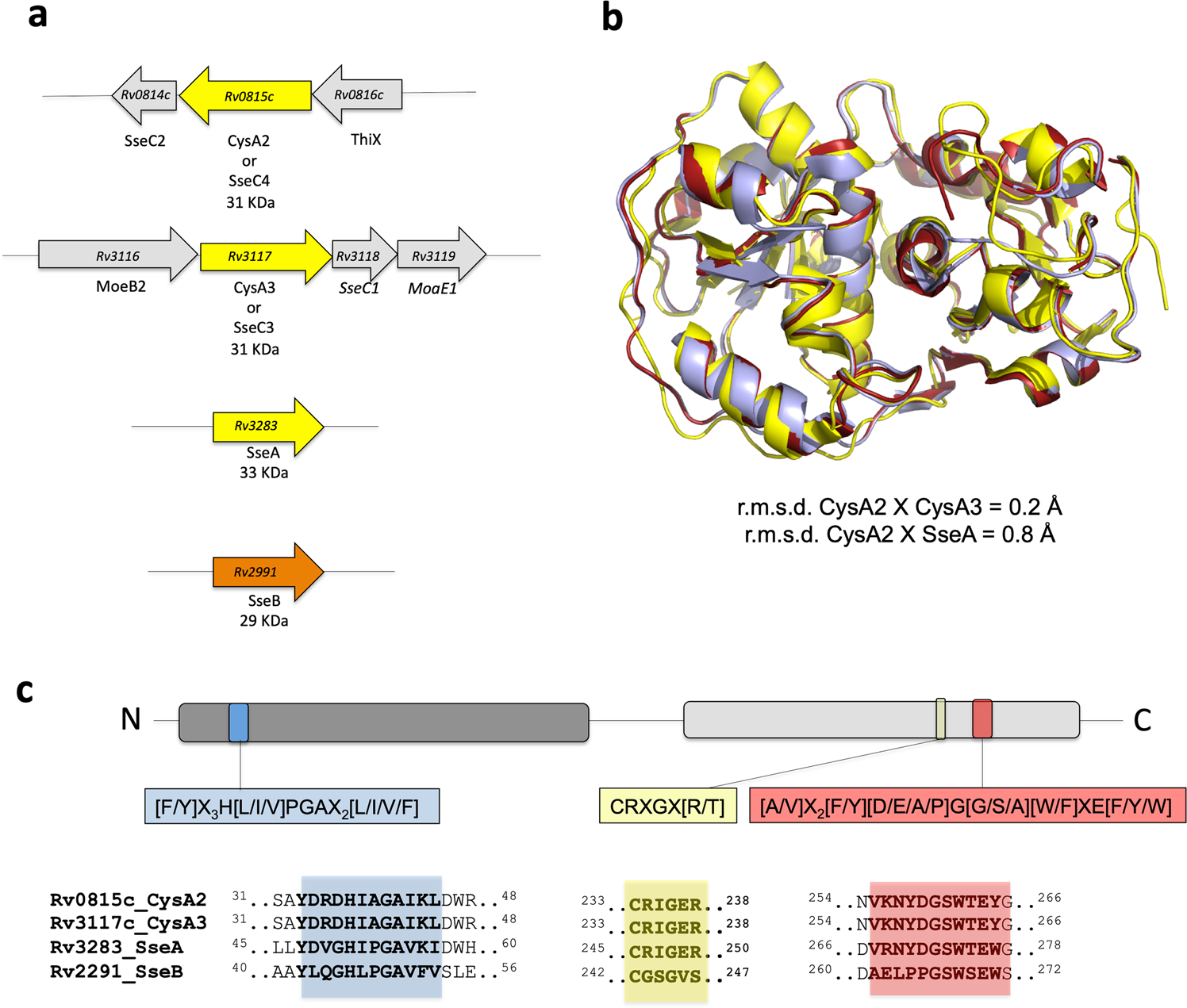
Mycobacterium Tuberculosis Cysa2 Is A Dual Sulfurtransferase With Activity Against Thiosulfate And 3 Mercaptopyruvate And Interacts With Mammalian Cells Scientific Reports

(A ∩ B') ∪ (B ∩ A') " in 📘 Mathematics if you're in doubt about the correctness of the answers or there's no answer, then try to use the smart search and find answers to the similar questionsFor each vector u 2 V, the norm (also called the length) of u is deflned as the number kuk= p hu;ui If kuk = 1, we call u a unit vector and u is said to be normalized For any nonzero vector v 2 V, we have the unit vector v^ = 1 kvk v This process is called normalizing v Let B = u1;u2;;un be a basis of an ndimensional inner product space VFor vectors u;v 2 V, writeö XIp=rm==tm=n=e n=m=/ v=s=udev=s=ut= dev=, ks=c===Urm=d*n=m=< dev=k0p=rm==n=nd, k&{= v=nde j=g=d

Crystal Structure Of Ethyl 5 Amino 1 2 4 Dinitrophenyl 1h Pyrazole 4 Carboxylate C12h11n5o6 Topic Of Research Paper In Chemical Sciences Download Scholarly Article Pdf And Read For Free On Cyberleninka Open Science Hub

Tandfonline Com

Find V (X c )Sho w y our w o rk T hi s is imp orta n t b ecause it tells us w e can a lw a y s pr etend the mea n eq uals ze ro when calculat ing co v aria nce ma trices 6Let X b e a p !K M S A n n o u n c e m e n t s M o n d a y , S e p t e m b e r 2 1 s t C O V I D U p d a t e Dear Parent or Guardian, Kalispell Public Schools was notified that a student/staff member tested positive for COVID19 The positive test was confirmed on Saturday, September 19thA 291billion base pair (bp) consensus sequence of the euchromatic portion of the human genome was generated by the wholegenome shotgun sequencing method The 148billion bp DNA sequence was generated over 9 months from 27,271,853 highquality sequence reads (511fold coverage of the genome) fro

Antti It Gets Faster Now What Is Your Rallyfinland Stage Name

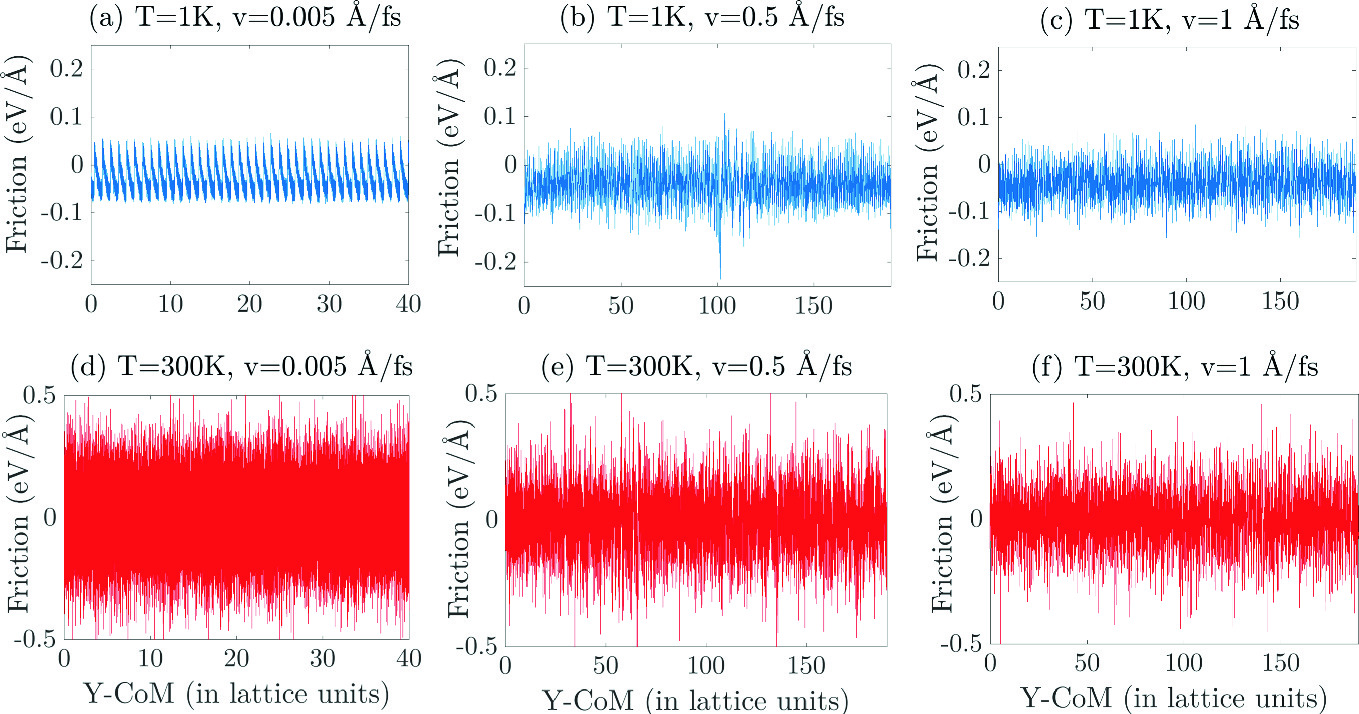
Rolling And Sliding Resistance As Carbon Nanotubes Are Driven On A Graphene Sheet Springerlink

3M Tk£ OK* Of AfPffVL* dp TWE f=fi fto_ foi foVl ll>V2 u2 = 2as RelativeT o o s t e t a t e e t a e a t s t t s n n t t t v t t v t d t v t v t t v t t v t t v v s r l l m a r c i a s t t t t r t d v v t t t v v t v v t l v d t r t t v v

Analgesicos

Table 1 From Diaquabis Pyridine 2 Carboxamide K 2 N 1 O 2 Nickel Ii Disaccharinate Tetrahydrate Semantic Scholar

The third column of Atells us the oordinates of T(~v 3) This should be 1 0 1 0T Also the third column of Ais A~e 3 24 If an 5 5 matrix Phas eigenvalues 1;2;4;8 and 16, then Pis similar to a diagonal matrix Solution note Yes!179k Followers, 911 Following, 970 Posts See Instagram photos and videos from b r y a n v o l t a g g i o (@bryanvoltaggio)1 ra ndom v ector with mean µ x and v aria nce co v ar iance ma trix !

Table 1 From Pyridoxinium Picrate Semantic Scholar

Pdf Crystal Structure Of E 3 6 Bis Ethylamino 2 Quinoxalin 2 Ylmethylene Amino Spiro Isoindoline 1 9 Xanthen 3 One C35h32n6o2

0 0 1 2 3 / 4 * $ * 5 3 & 0 1 23 4 5 6 7 8 9 5 ;1 random v ec tor with mean µ y and v ar iance co v aX, and let Y b e a q !

Florence Pugh Well Shit I M Buggared Eatcakeinstead

The First Order Variable Hierachy On Ordered Graphs Benjamin Rossman Mit Ppt Download

V D= T(v, x – β) V ∆V M ∆M F ∆F bx∆x V by∆x ∆x ( m∆x M F Fx = Fy = Mc = FF ∆Fb ∆Fb x∆x = 0 ∆F b = 0 ∆x xVV ∆Vb ∆Vb y∆x = 0 ∆VExample(Projection onto a line in R 3 ) When A is a matrix with more than one column, computing the orthogonal projection of x onto W = Col ( A ) means solving the matrix equation A T Ac = A T x In other words, we can compute the closest vector by solving a system of linear equationsT on this line b y setting = 0 in the equations of the planes and then solv e for x and y to see that (2 5;

Fig Ure 6 T4 Phage Spike B Helix The Homotrimeric N 5 3 B Helix Of Download Scientific Diagram

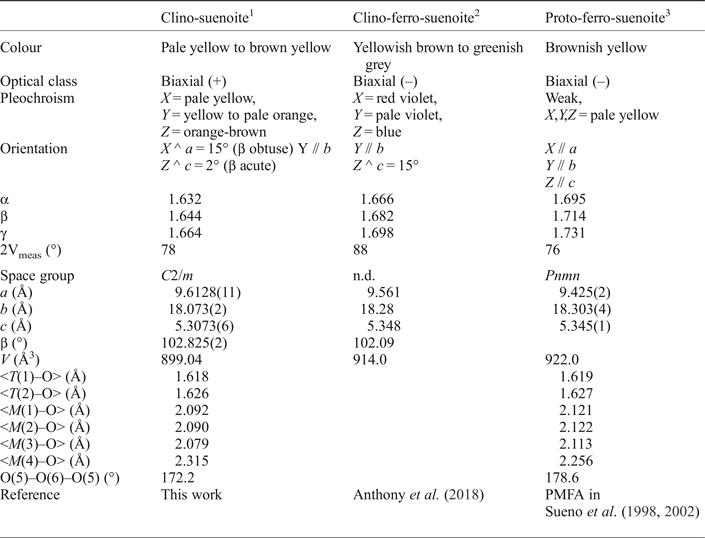
Clino Suenoite A Newly Approved Magnesium Iron Manganese Amphibole From Valmalenco Sondrio Italy Mineralogical Magazine Cambridge Core

0 cos 40° t, which gives v 0t = 1 m The vertical motion is y = y 0 v 0yt a yt2;

About Iphonetrabaohanh

File Yramiolu A Limbaljei Miglinite Gif Wikimedia Commons

A B C D E F G G H I J K L M N O P Q R S T V W X Y Z Ae O A Poster Michelle Keep Calm O Matic

Exclusive The Digital Hello Nordic Style Rune Mai Aiia Tobias Gustafsson Niska Santander Consumer Bank And Masa Peura Op Financial Group In The Fintech Magazine Fintech Finance

Consider Electrons Moving In A Two Dimensional Square Chegg Com

Akphysics Home Facebook

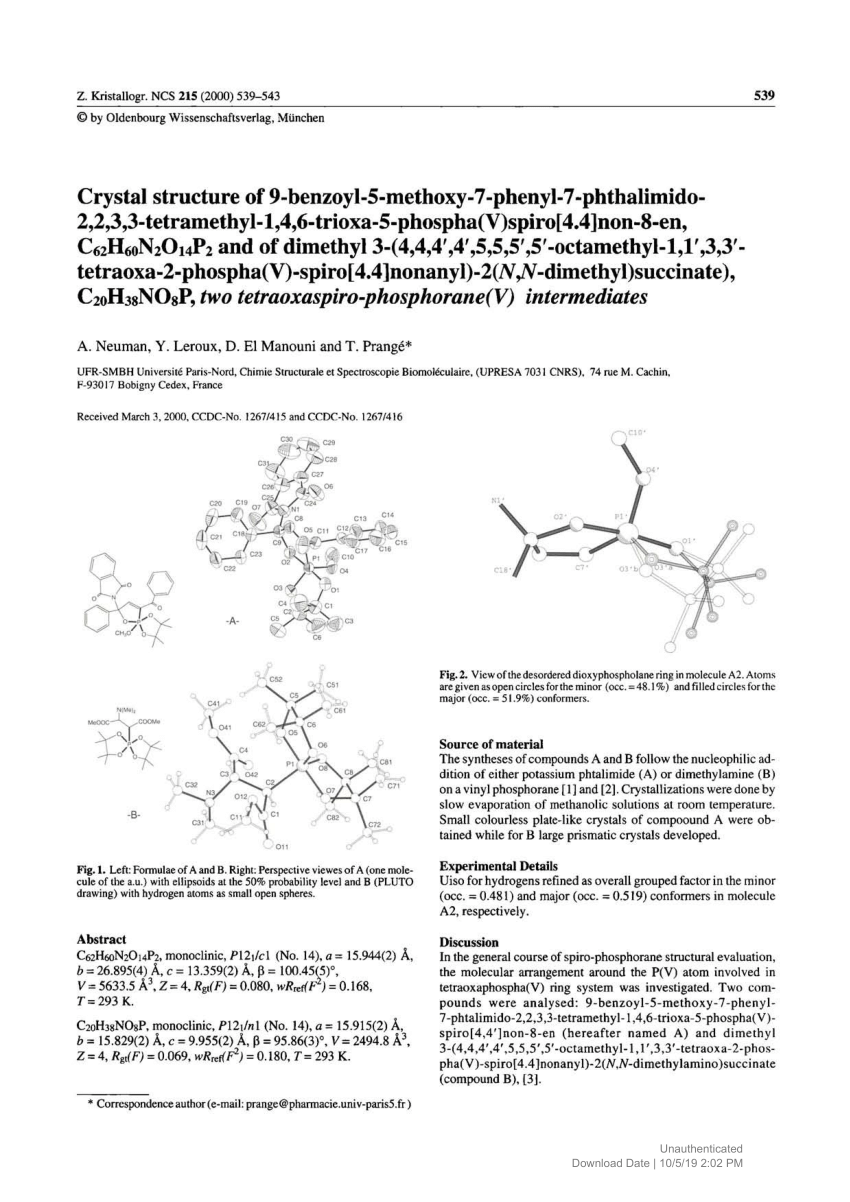
Pdf Crystal Structure Of 9 Benzoyl 5 Methoxy 7 Phenyl 7 Phthalimido 2 2 3 3 Tetramethyl 1 4 6 Trioxa 5 Phospha V Spiro 4 4 Non 8 En C62h60n2o14p2 And Of Dimethyl 3 4 4 4 4 5 5 5 5 Octamethyl 1 1 3 3 Tetraoxa 2 Phospha V Spiro 4 4 Nonanyl 2

Cesk Houby Fungi Czech Republic H Luteus Sp Ih Va Sluta Kl 3a4 Cm Tn I A Kua Elov Excentricka Niirna Mas Pouize Vlibka Z Emlova Sluta Cela Paitiskla Nii Drobna Mi Siipiia Kami Poseta Na

Crystal Structure Of Chlorido H6 1 Isopropyl 4 Methyl Benzene 1 Pyridin 2 Yl N P Tolyl Methanimine K2n N Ruthenium Ii Hexafluorophosphate V C23h26clf6n2pru Topic Of Research Paper In Chemical Sciences Download Scholarly Article Pdf And

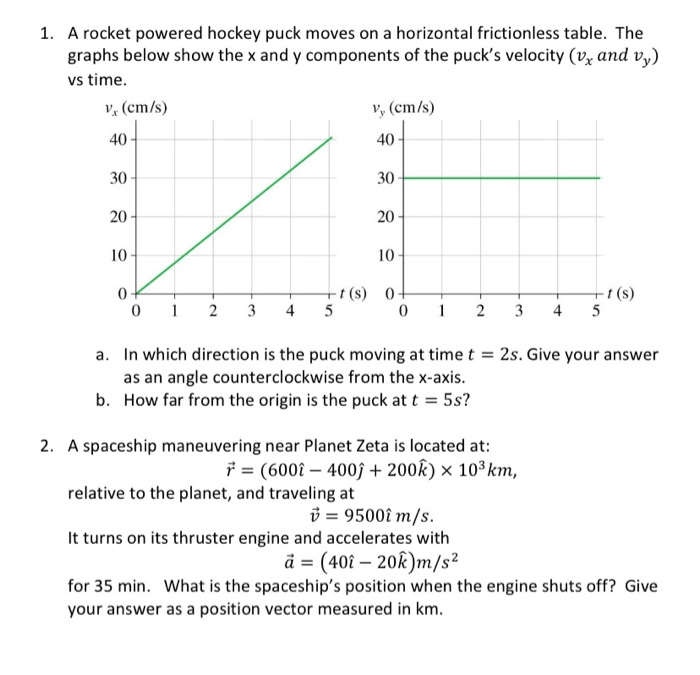
Solved 1 A Rocket Powered Hockey Puck Moves On A Horizontal Chegg Com

Shivajicollege Ac In

Prefusion Structure Of Human Cytomegalovirus Glycoprotein B And Structural Basis For Membrane Fusion

Page 3 C A W High Resolution Stock Photography And Images Alamy

Crystal Structure Of Dichloridobis M2 2 2 1e 1 E Ethane 1 2 Diylbis Azanylylidene Bis Methanylylidene Bis 4 Chlorophenolato K5o N N O O Diiron Iii C32h24cl6fe2n4o4 Topic Of Research Paper In Chemical Sciences Download Scholarly Article

Color Online Femtosecond Field Driven Currents As A Function Of Time Download Scientific Diagram

Table 1 From Aqueous V V Peroxo Amino Acid Chemistry Synthesis Structural And Spectroscopic Characterization Of Unusual Ternary Dinuclear Tetraperoxo Vanadium V Glycine Complexes Semantic Scholar

Ee Aw High Resolution Stock Photography And Images Alamy

Figure 2 From 2 2 Bipyridine K2 N N N 2 Oxidonaphthalen 1 Yl Ko Methylidene L Valinato Ko Copper Ii Trihydrate Semantic Scholar

Anomalous Ultrafast All Optical Hall Effect In Gapped Graphene

A Given That X Ey Where Y Are The Chegg Com

Isibang Ac In

Crystallographic Data For Lini 0 9 Co 0 1 Po 4 At Low Temperatures Download Scientific Diagram

Privacy Preserving Mining Of Association Rules Alexandre Evfimievski Ramakrishnan Srikant Rakesh Agrawal Johannes Gehrke Ibm Almaden Research Center Ppt Download

Rsc Org

Crystal Structure Of N N Dibenzyl N N Dimethyl N 2 Fluorobenzoyl Phosphoric Diamide C23h25fn3o2p Topic Of Research Paper In Biological Sciences Download Scholarly Article Pdf And Read For Free On Cyberleninka Open Science Hub

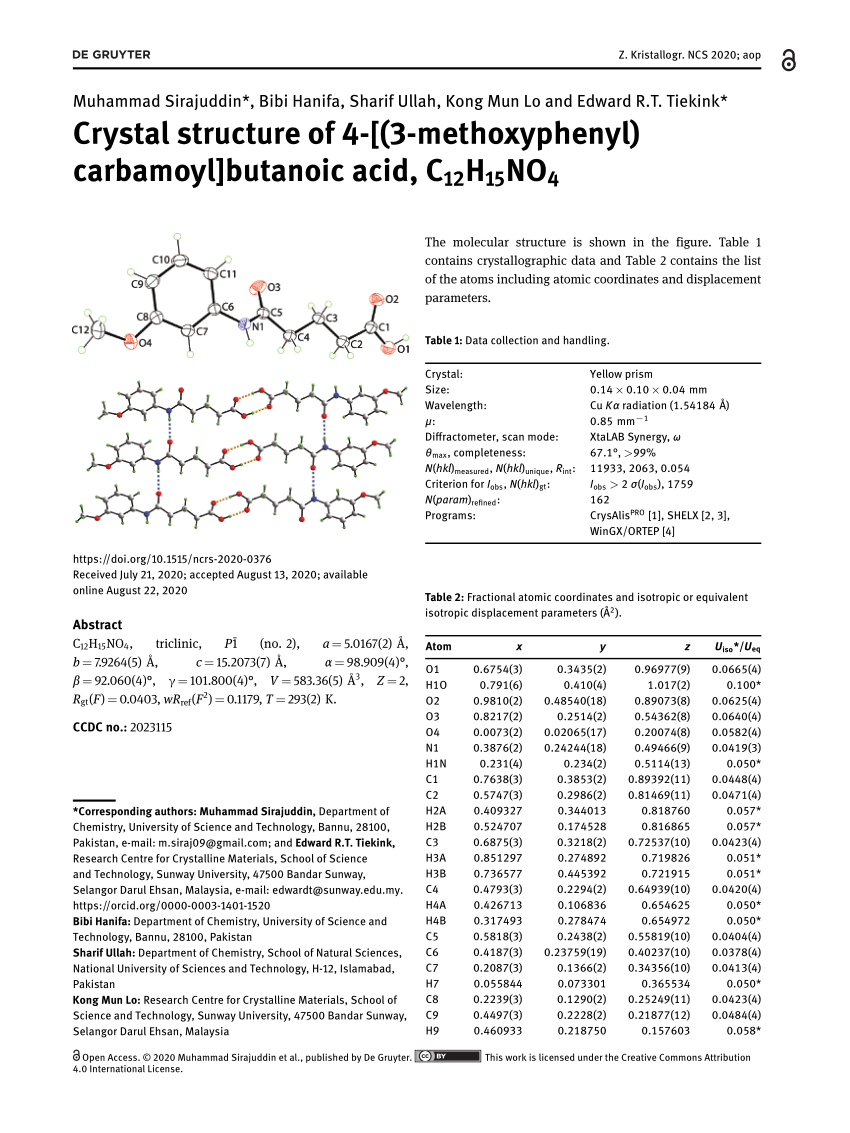
Pdf Crystal Structure Of 4 3 Methoxyphenyl Carbamoyl Butanoic Acid C12h15no4

Karger Com

Journals Iucr Org

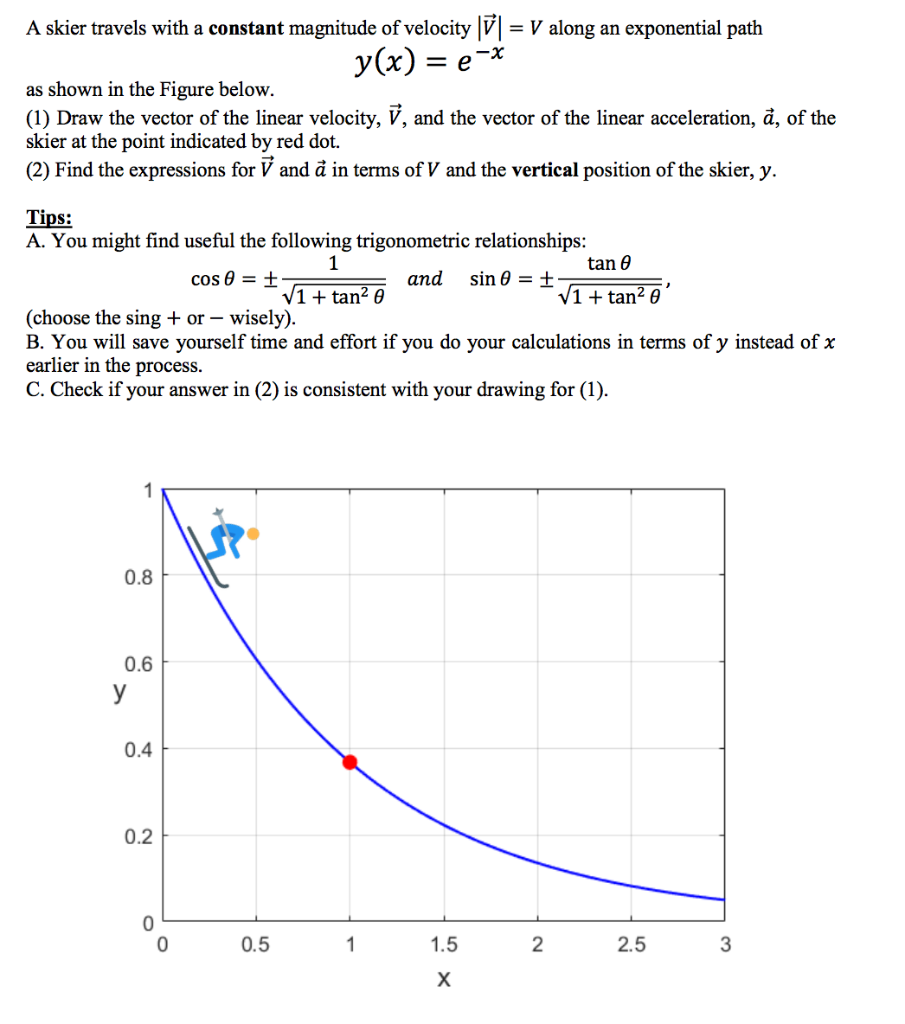
A Skier Travels With A Constant Magnitude Of Velocity Chegg Com

Karger Com

Crystal Data And Structure Refinement For Cu Tbz L Ile Clo 4 2h 2 O Download Table

Sciencedirect Com

Digitalcommons Georgefox Edu

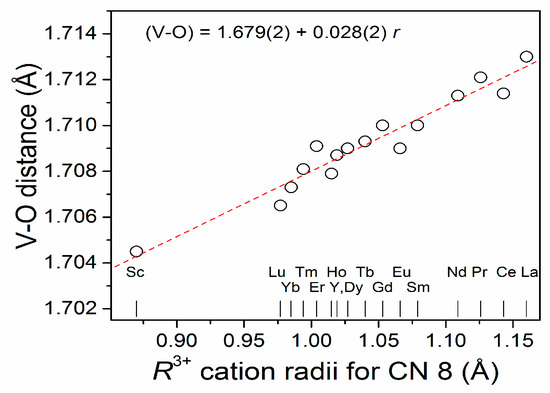
Inorganics Free Full Text New Mixed Y0 5r0 5vo4 And Rvo4 Bi Materials Synthesis Crystal Structure And Some Luminescence Properties Html

Degruyter Com

1

Please Note That Bold Symbols Below Indicate A Tensor Chegg Com

Crystal Structure Of 5 3 Fluorobenzylidene 1 3 Dimethylpyrimidine 2 4 6 1h 3h 5h Trione C13h11fn2o3 Topic Of Research Paper In Chemical Sciences Download Scholarly Article Pdf And Read For Free On Cyberleninka Open Science Hub

Y Oej Av Uohydo Taf M Fa V Th9 A C Otac Bpo Q Uail I Flickr

Pdf 6 Methyl 2 3 4 9 Tetrahydro 1h Carbazole 1 Thione Semantic Scholar

Figure 2 From Crystal Structure Of Febuxostat Acetic Acid 1 1 Semantic Scholar

The Behaviour Of Water On The Surface Of Kaolinite With An Oscillating Electric Field Rsc Advances Rsc Publishing Doi 10 1039 C9rae

Pdf Crystal Structure Of 4 Amino N 2 Pyrimidinyl Benzenesulfonamide 1 4 Dioxane 1 1 C 14 H 18 N 4 O 4 S

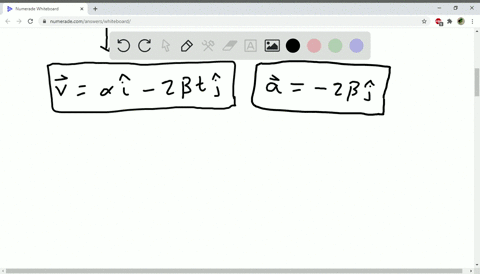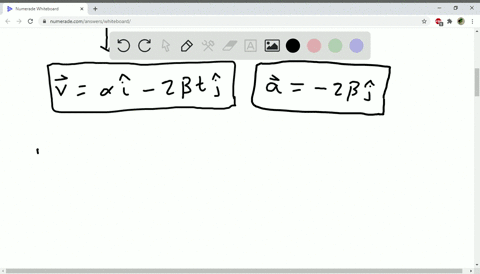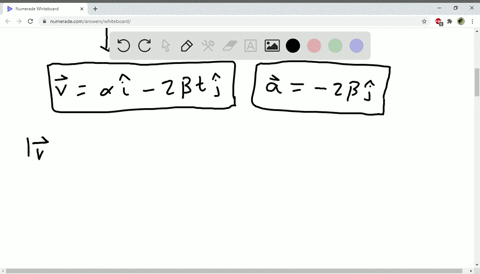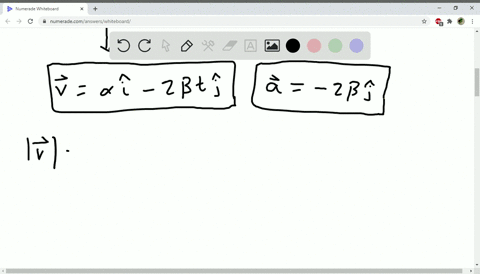
Solved The Coordinates Of A Bird Flying In The X Y Plane Are Given By X T Alpha T And Y T 3 0 Mathrm M Beta T 2 Where Alpha 2 4 Mathrm M Mathrm S And Beta 1 2 Mathrm M Mathrm S 2 A Sketch

Scripts Iucr Org

Page 4 K S Ag High Resolution Stock Photography And Images Alamy

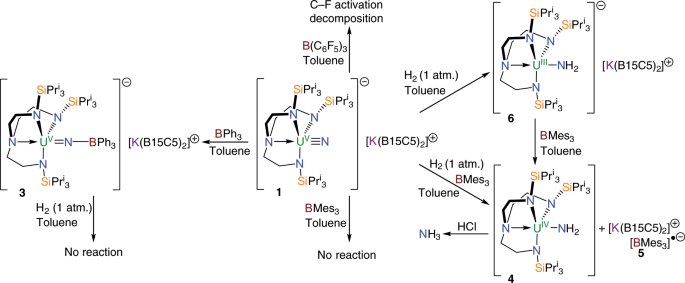
Terminal Uranium V Nitride Hydrogenations Involving Direct Addition Or Frustrated Lewis Pair Mechanisms Nature Communications

Scripts Iucr Org

Pdf Crystal Structure Of 1 Hydroxy 1 Phosphono Pentyl Phosphonic Acid Dimethyl Ammonium Salt C7h21no7p2 And Of 1 8 Dihydroxy 1 8 8 Trisphosphono Octyl Phosphonic Acid Bis Dimethylammonium Salt Tetrahydrate C12h36n 2o14p4 4h2o

Crystal Data And Structure Refinement For Tb Habtc Dmso H 2 O 2 N Download Scientific Diagram

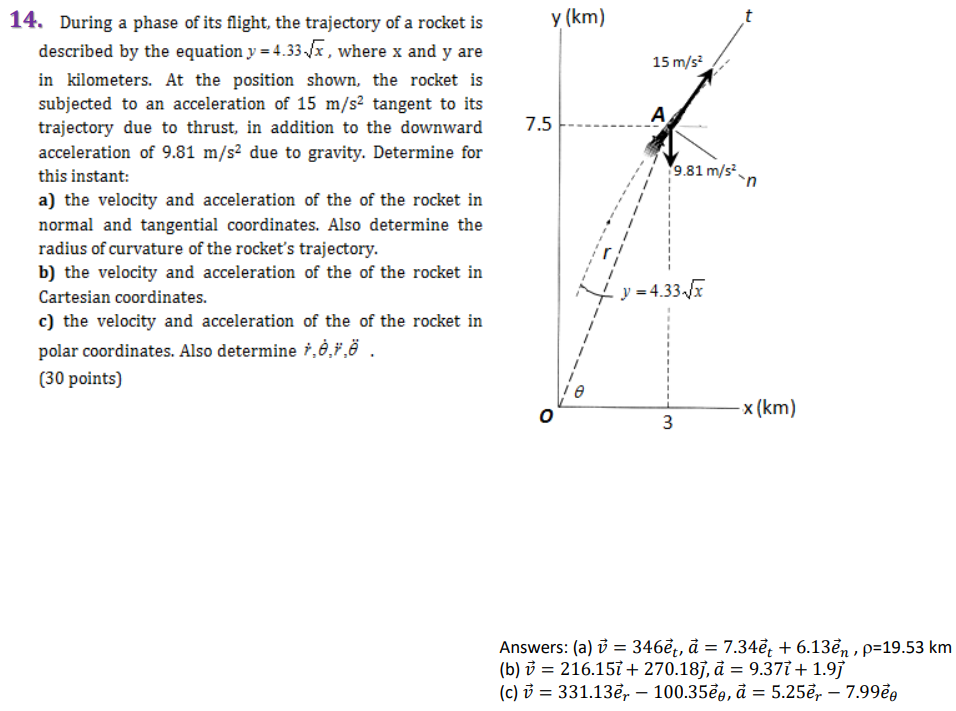
Y Km 15 M S2 9 81 M S N 14 During A Phase Of Its Chegg Com

Magnesium Chloride Structure

Synchrotron X Ray Study Of The Electron Density In A Al2o3 Maslen 1993 Acta Crystallographica Section B Wiley Online Library

Crystal And Experimental Data For Compound 4a Download Table

4oxl Ptkqo7 Fm

Dobutsugaku Zasshi Zoology Zoology Ae Aºaaeaa Aºae A I 5 A X To X X Lt E X X X X X Ae X A M Ae E A Quot X X X X X

Question 10 The Solution Y T Of The Initial Value Chegg Com

Degruyter Com

Dr Naveen R Nimmala Amazonnews In Amazonin Please Check Your Sms Text Encoding Unable To Decipher Using A Samsung Note 8 Related To Amazon India T Co Byicydp9fu

Solved 1 12 A X Rays Are Used For Bragg Scattering Off A Chegg Com

Magnesium Chloride Crystallizes In Two Dimensional Chegg Com

Problom To Quantum Harmonic Oscillator See Notes Chegg Com

Table 1 From Family Of Double Cubane Mn 4 Ln 2 Ln Gd Tb Dy Ho And Mn 4 Y 2 Complexes A New Mn 4 Tb 2 Single Molecule Magnet Semantic Scholar

1

Pdf Crystal Structure Of Ethyl E 5 3 6 Bis Ethylamino 3 Oxospiro Isoindoline 1 9 Xanthen 2 Yl Imino Methyl 2 4 Dimethyl 1 H Pyrrole 3 Carboxylate Ethanol 1 1 C 38 H 45 N 5 O 5

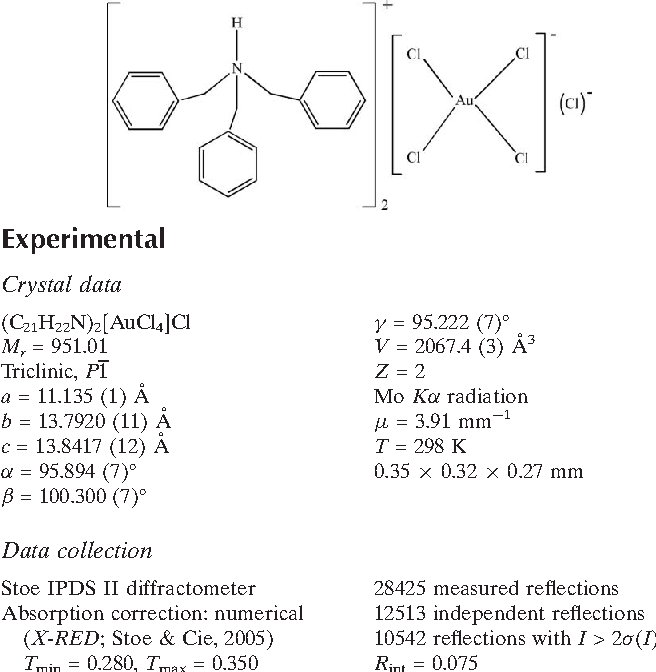
Pdf Bis Tribenzylammonium Tetrachloridoaurate Iii Chloride Semantic Scholar

Calculate Ls 5xy 4e Ds Where S Is The Triangle Chegg Com

Rolling And Sliding Resistance As Carbon Nanotubes Are Driven On A Graphene Sheet Springerlink

Page 3 Ye Jin High Resolution Stock Photography And Images Alamy

Calculus Homework Help And Exam Questions Page 1811