画像をダウンロード 円 三角形 角度 101448-円 内接 三角形 角度
問題3 下の図の角xの角度を求めなさい。 → 解答 問題4 下の図の角xの大きさを求めなさい。ただし、同じ印の付いた角の大きさは等しいものとします。解答 補足 三角形の外接円の応用例としてよく知られているのは、 計算幾何学の分野に現れるポロノイ図である。 ボロノイ図は生物の縄張りをシミュレーションしたり、 点群と内接する最大円を求める際に使われるなど応用例が多岐にわたる。 円Oの中心点Oを使って三角形ABCを3分割する。 三角形ABC = 三角形OAB 三角形OBC 三角形OCA 円Oの半径をxとして、三角形の面積の公式に当てはめる。 44*28/2 = 28x/2 44x/2 522x/2 616 = 621x x = 99cm 円周を求める 99 * 2 * 314 = 622 cm

円周角の定理と証明 中心角の求め方を詳しく解説 Rikeinvest
円 内接 三角形 角度
円 内接 三角形 角度-入試解説 6年生 男子校 5年生 正方形 正三角形 東京 兵庫 灘 算数オリンピック 面積比 共学校 円 図形NOTE logix出版 角度 1日目 相似 長方形 直角三角形 4年生 女子校 立方体 おうぎ形 30度 正六角形 16年 17年 19年 トライアル 18年 年 二等辺三角形角度がまとめられれて、 しかもそれが一直線上にあれば求めるのは簡単です。 一直線の角度とは、すなわち180度ですからね。 したがって 三角形の内角の和=180度 となるのです。




接線の性質 なぜこの記号同士が同じ角度になるのかが分かりません Clearnote
円や角度に関する作図はこちらもご参考ください(^^) 円の中心を作図する方法とは? 難問円に内接する正三角形の作図方法とは? 角度15°・30°・45°・60°・75°・90°・105°の作り方とは?三角形の3辺から角度を計算 答えの度分秒(° ′ ″ )は、秒の小数点以下2桁まで求めています。 水平線までの距離を出すプログラムを作るのに参考にした。 わかりやすくて便利ですね。 台形型の部屋の変形のコーナーに壁にピッタリと合った棚を三角形abc で,頂点a, b, c に対する辺の長さ を,それぞれ,a, b, c とする。また∠a, ∠b, ∠c の 大きさを,それぞれa, b, c と書くことにする。 このとき次の定理が成立する。 ここでr は三角形abc の外接円の半径である。 証明 外接円の中心をo とする。
外心の角度の関係 その1 ABCの外心Oをとして、外心O が ABCの内部にあるとき、外 接円の半径から、3つの二等辺 三角形がある。その底角を図の ようにa,b,c,とすると、 2a+2b+2c=180° 2でわっ2年生で学んだ四角形のココと 全く同じですね ・x=abc ( 四角形の外側の角) 《 例 》 円周を8等分した点です x, y, z の角度を求めましょう →1コマあたりの中心角は 360°÷8 = 45° xは3コマ分の中心角の半分 (=円周角) → x = 1 2 1 2 (3×45°) = 135° 2 135 ° 2 = 675°正三角形を作ることができる というわけですね。 作図手順の解説 それでは、まず円を6等分していきましょう! そのためには、円の中心を求める必要があるので 円の中心を作図してやります。 円の中心は、円周上のどの点からも等しい距離にある点です。
今回は、角度だけに絞って この正五角形を見てみますと このようになります。 ここで rs//pq です。 ocdの底角を計算するときも、 この ocdをタテ半分に分けて、直角三角形を作り 90-36 で、54° これなら 暗算でできそうですね。三角形の面積は「 \(底辺×高さ÷2\) 」という公式から求まりますが、この公式以外にも色々な方法で三角形の面積を求めることができます。 このページでは、そんな三角形の面積の求め方をタイプ別に見ていきましょう。 このように、三角関数の角度は単位円に条件を書き込んでいくだけで求められます。 範囲や値の条件を見落とさないようにすることだけ注意しましょう! 三角関数の角度の計算問題 それでは、実際に三角関数の角度の計算問題を解いていきましょう!




円周角の定理 角度の計算 中学数学 Youtube



1
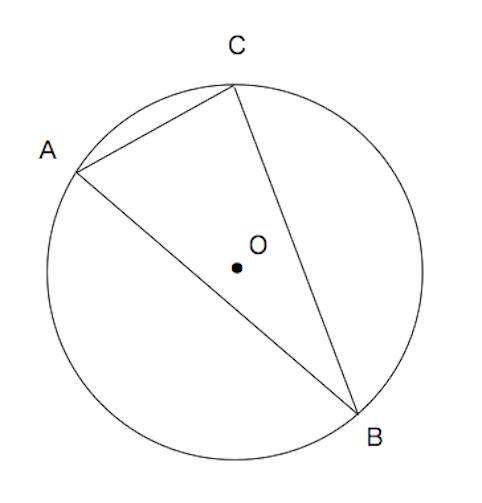
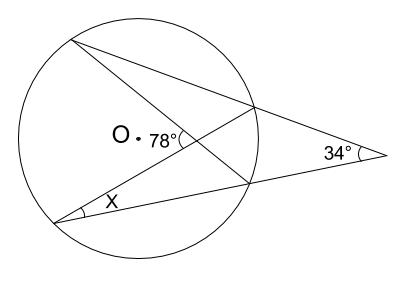
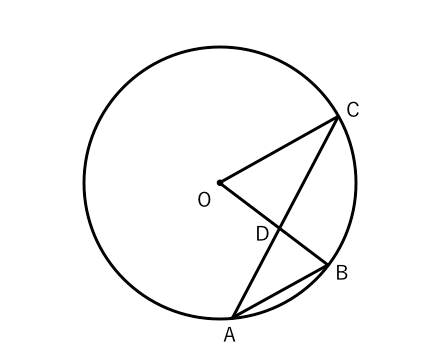
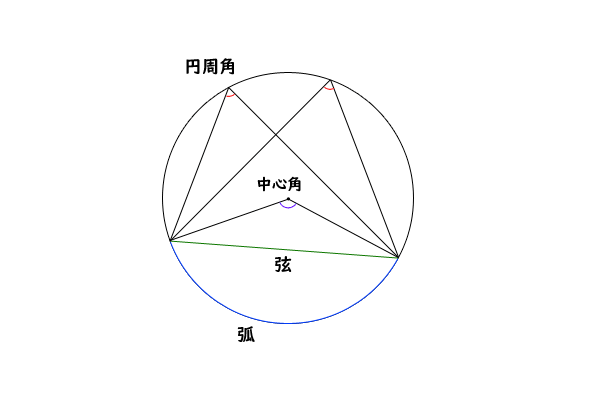
工夫していろいろな角度を求める問題です。 平面図形の問題の中でも学習はしやすいところです。 角度の問題は、同じようなパターンの問題をまとめて解いてコツをつかんでいくようにしましょう。 例1)正三角形や正方形を組み合わせた 数学 中学数学 円の中の三角形の角度の問題 お世話になります。 円の中の三角形の角度の問題ですが、導き方がわかりません。 問題 図は円の中心o点を通る直線を引き、円との交点をそれぞれa、cと 質問no979一つの弧に対する「円周角」の大きさは,「中心角」の半分になります. OC=OB= (半径)だから OBCは二等辺三角形になる. 二等辺三角形の2つの底角は等しいから ∠ B=∠ C (1) ∠ BOA=∠ B∠ C (2) 差で示します. 中心角92°が書いてあって,円周角が




6本の缶を最短の紐で束ねる意外な方法とは 円と球の不思議な雑学 横山 明日希 ブルーバックス 講談社 1 4



第120問の解答
円の特徴 ここでは、同じ弦をもつ三角形に外接している円の特徴について説明しましょう。 図のように円の中に ABP、 AQB、 ABRがあるとします。 この三角形はABを共通の底辺としてもっていますね。 このような状況にあるとき、∠APB=∠AQ 三角形の外角の和は、接しない他の2角の和でしたよね? 角度1:等しい角度3つと角度の性質3つ 上記のテクニックももちろん使えますが、 補助線を引く というの は図形問題の基本なので、そちらも頭に絶えず入れて考えましょう。 円と角度の中学入試問題等一般に,高校入試問題では「円周角の定理」を覚えているだけでは,問題は解けません.この問題では,次の2つの定理を組み合わせて解いています. (1) 一つの弧に対する円周角は等しい. (2) 三角形の内角の和は180°になる. 右の図のように,円周上に4




6本の缶を最短の紐で束ねる意外な方法とは 円と球の不思議な雑学 横山 明日希 ブルーバックス 講談社 1 4
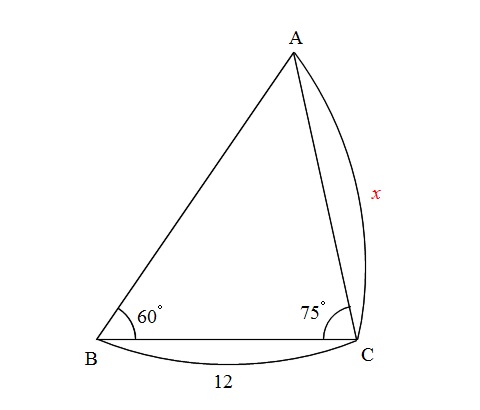



三角形で角度が2つ分かっているのに正弦定理も余弦定理も使えない
問題 下の図のような三角形に内接する円の半径を求めなさい。 解答 超有名問題です。 \(2\) つの解き方を示します。 必ずどちらも理解・暗記しておきましょう。 解法1 円と接線の性質 円の中心と接点を結ぶ線分(半径)は 実際に 単位円 を書き、 三角形の比 から角度を求めてみましょう。 ここでも三角形の比が\(1\sqrt{3}2\)であるとわかるので、角度が求められますね。 このようにθ=60°,300°は\(cosθ=\frac{1}{2}\)を満たすことがわかります。接弦定理 円Oの弦ABとその端点Aの接線ATがあるとする。 このとき、 がつくる円周角 は と等しくなる。 これを 接弦定理 と呼ぶ。 1 の場合 以下のように、円の中心Oを通る三角形 を考えます。 となります。 また、 は直角三角形なので




面積の移動 円周角 知能問題 数的処理 判断推理 数的推理 数学パズル spi 空間把握 解いてみてください
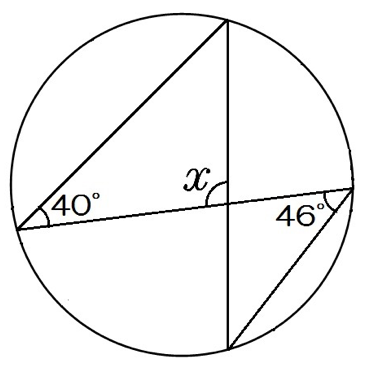



円の性質 円周角の角度の求め方の3つのパターン Qikeru 学びを楽しくわかりやすく
・直角三角形(高さと斜辺) 直角三角形の高さと斜辺から、底辺と角度と面積を計算します。 ・直角三角形(高さと角度) 直角三角形の高さと角度から、底辺と斜辺と面積を計算します。 正五角形というだけで 分かる角度は・・・ 内角 と 外角 って 何だっけ? 作図の考え方 ~ なんだ、そうだったのか! 対角線の数って どうやって計算するんだ? 円錐を カット する! 体積は どうなる? 円に内接する 三角形の 問題 3 台形と円の 今回は、三角形の角度を求める問題を解いていきたいと思います。 三角形の内角の和は180° 三角形の外角の大きさ=となり合わない2つの内角の和 三角形の角度を求める問題 問題① 問題② 問題③ 問題④ 三角形の角度を求める問題では、対頂角・同位角・錯角の性質や二等辺三角形の性質



1




円の特徴 同じ弦をもつ三角形 数学a By Okボーイ マナペディア
小学生の算数・図形・面積・体積に関する算数の問題プリント、練習プリントです。 無料でダウンロード、印刷してご利用いただけます。 小学1年生の算数 図形 練習問題プリント 小学2年生の算数 図形 練習問題プリント 小学3年生の算数 図形 練習問題 棒の角度はいつでも x 軸の正の向き(原点から右方向に延びる線)から計ると決められています。ということは、この図の場合、棒の角度は 90°θ と表されます。 同じような手法で、オレンジの三角形をさまざまな方法で置いていきます。
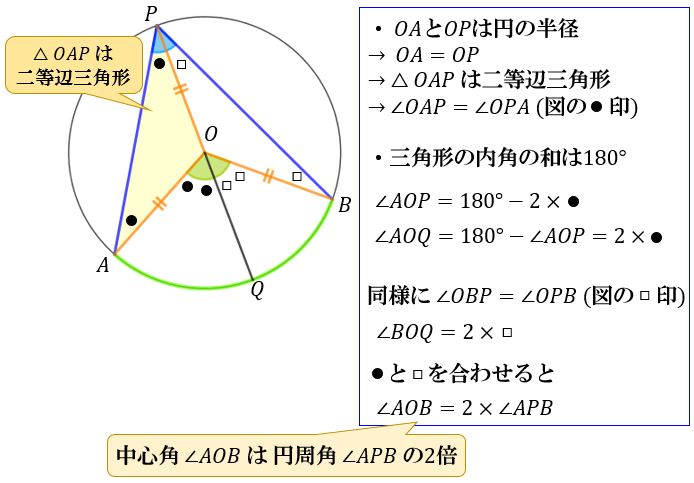



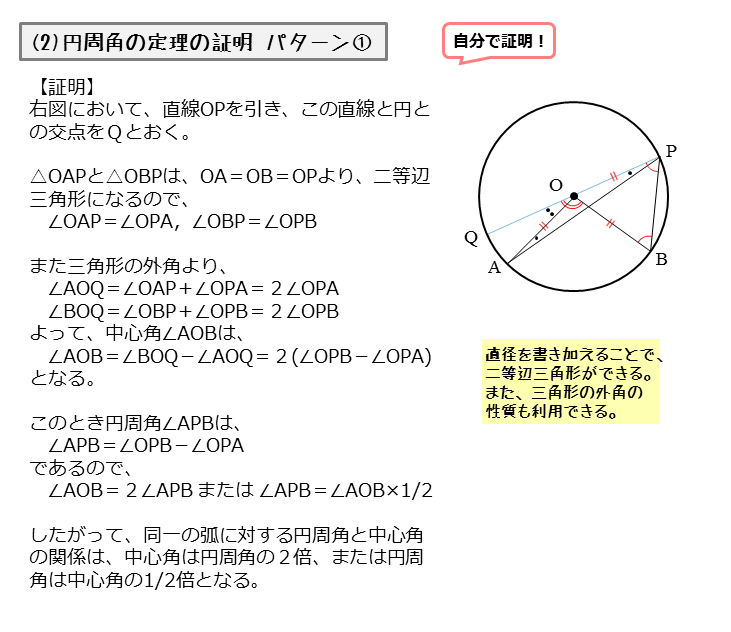
円周角の定理の証明 3つのパターンから分かる円周角と中心角の関係性 アタリマエ




勉強しよう数学 円の外の点に拡張した円周角の定理
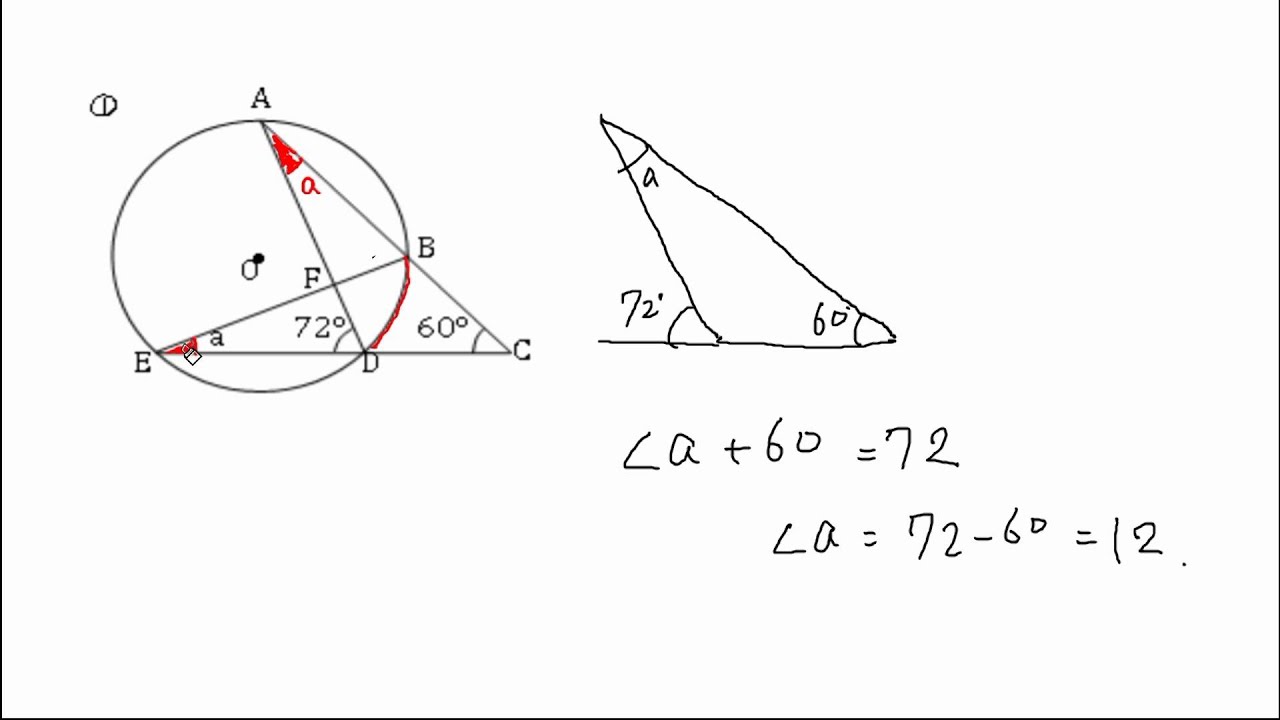



円周角の定理 問題 Youtube
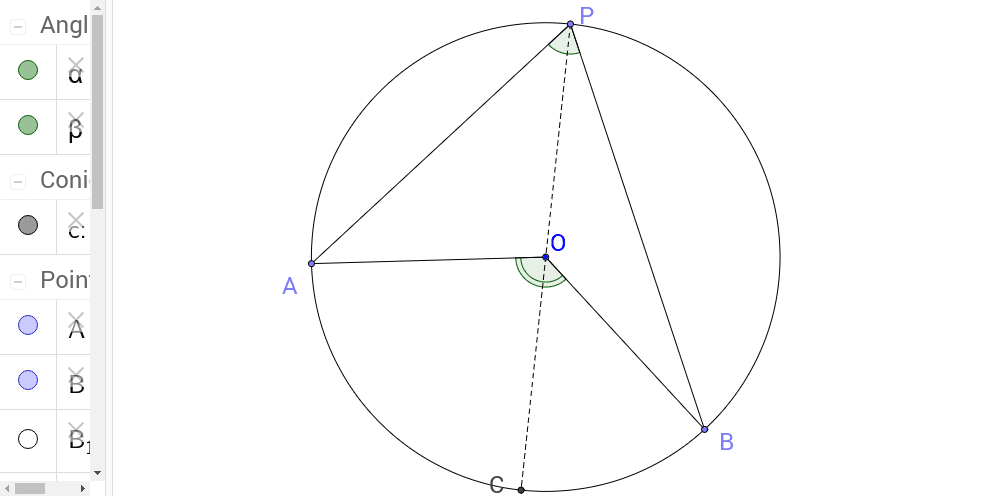



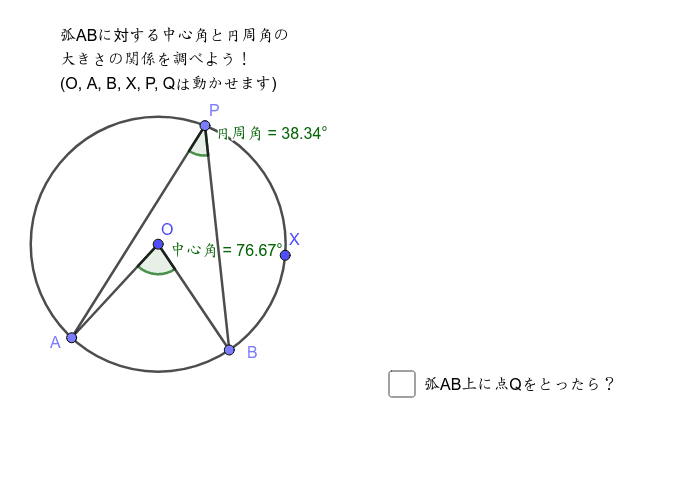
中心角と円周角 Geogebra



1
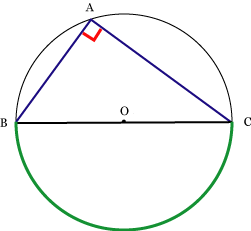



円周角の定理




接線の性質 なぜこの記号同士が同じ角度になるのかが分かりません Clearnote



同じ弧に対する円周角




円周角の定理と証明 中心角の求め方を詳しく解説 Rikeinvest
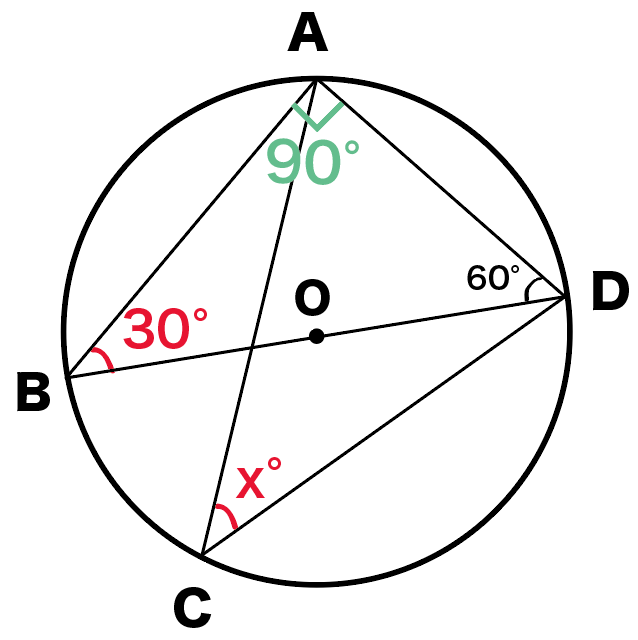



円周角の定理で角度を求める問題の解き方3ステップ Qikeru 学びを楽しくわかりやすく




円周角と円の外の点を結んで おときち副塾長 電脳空間学習塾かもん Youtube



円周角



円と三角形 角度 中学から数学だいすき




円の性質 円周角の角度の求め方の3つのパターン Qikeru 学びを楽しくわかりやすく
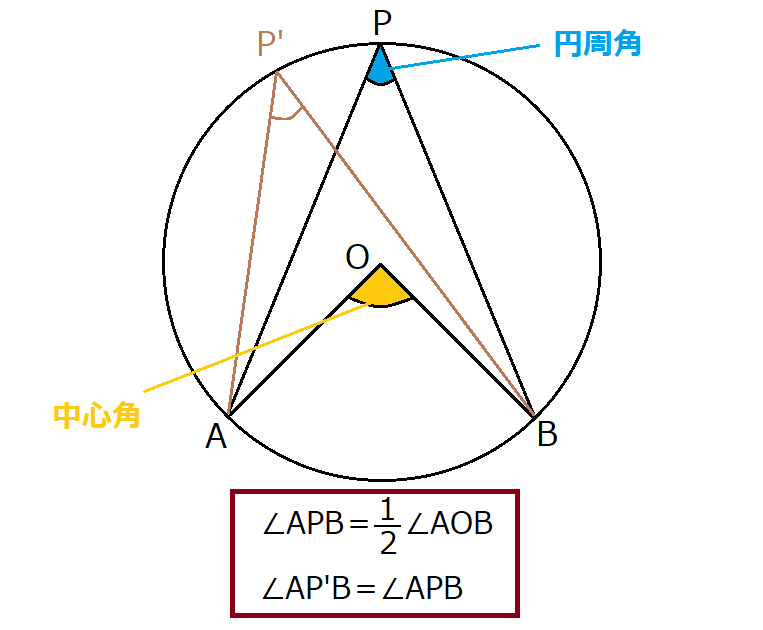



円周角の定理の証明を3つ紹介 逆も把握しよう ヒデオの情報管理部屋all Rights Reserved




円周角の定理と角度を求める問題10選 中心角 ターレスの定理 内接する四角形 教遊者
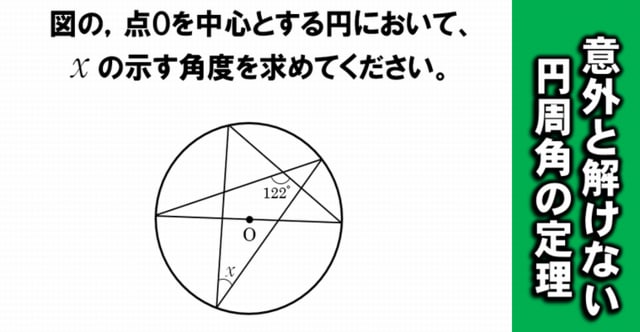



意外と解けない円周角の定理 中3レベルの数学問題 暇つぶしに動画で脳トレ
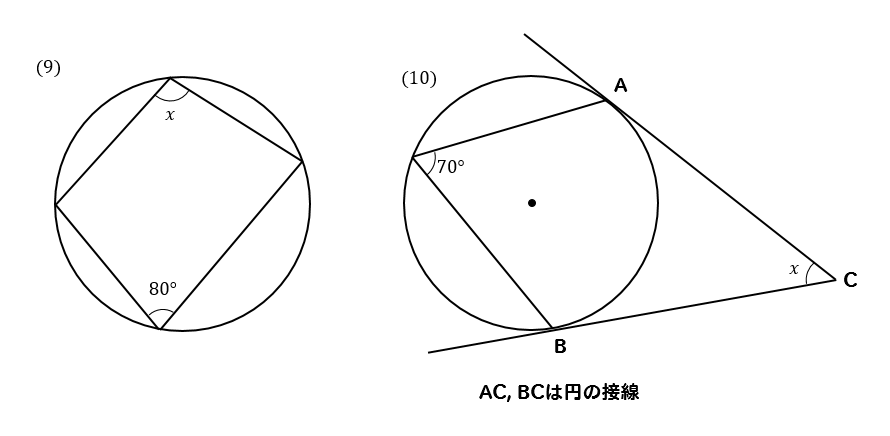



これで10点アップ 円周角の定理とは 問題の解き方はどうやるのかパターン別に解説 数スタ




円周角の定理とは 必ず押さえたい7つのポイント 遊ぶ数学
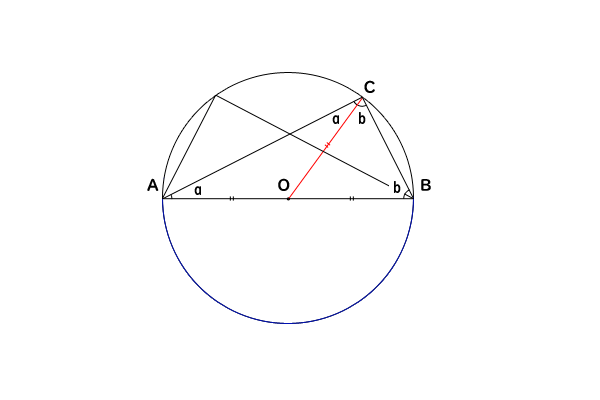



円周角の定理とその逆の証明 高校数学マスター
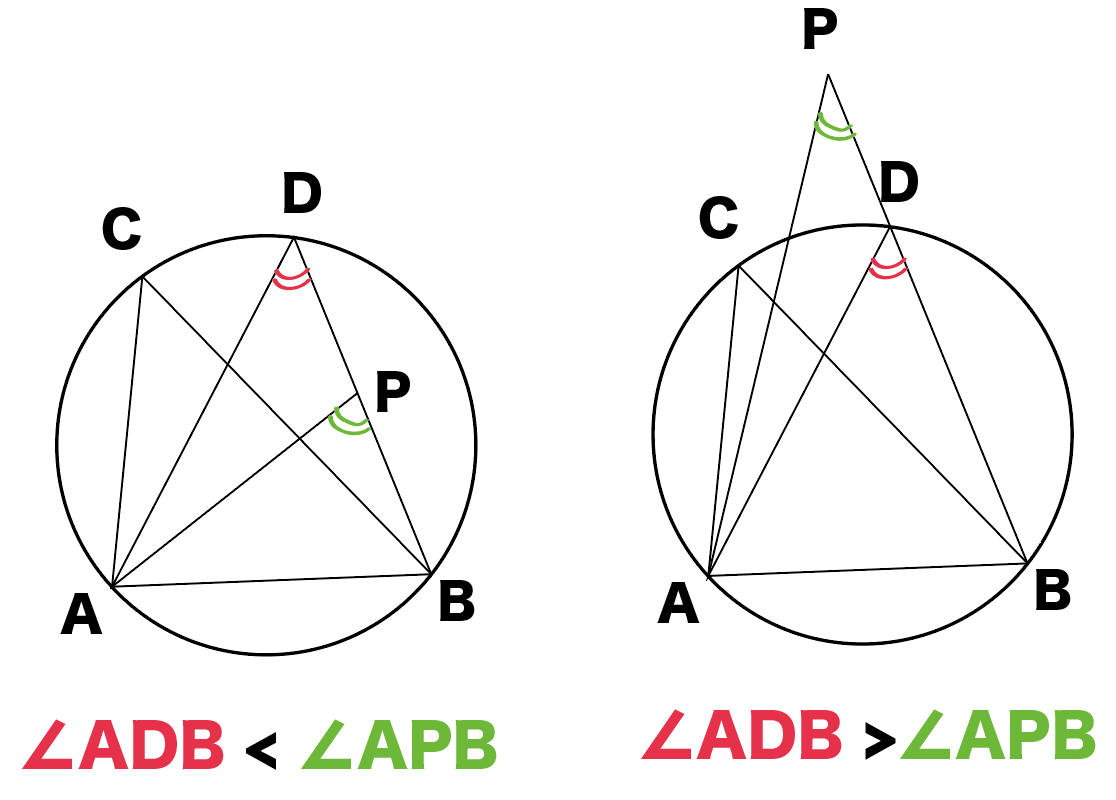



3分でわかる 円周角の定理の逆の証明 Qikeru 学びを楽しくわかりやすく



円周角
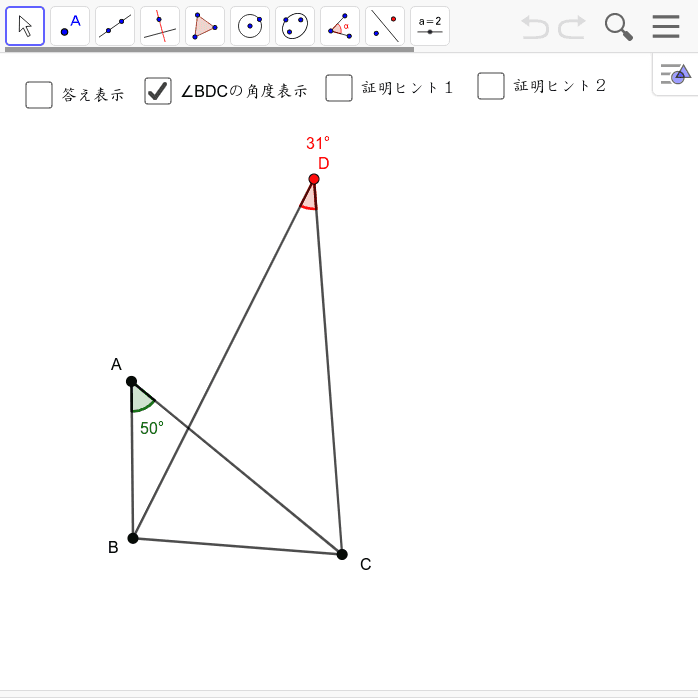



円周角の定理の逆 Geogebra
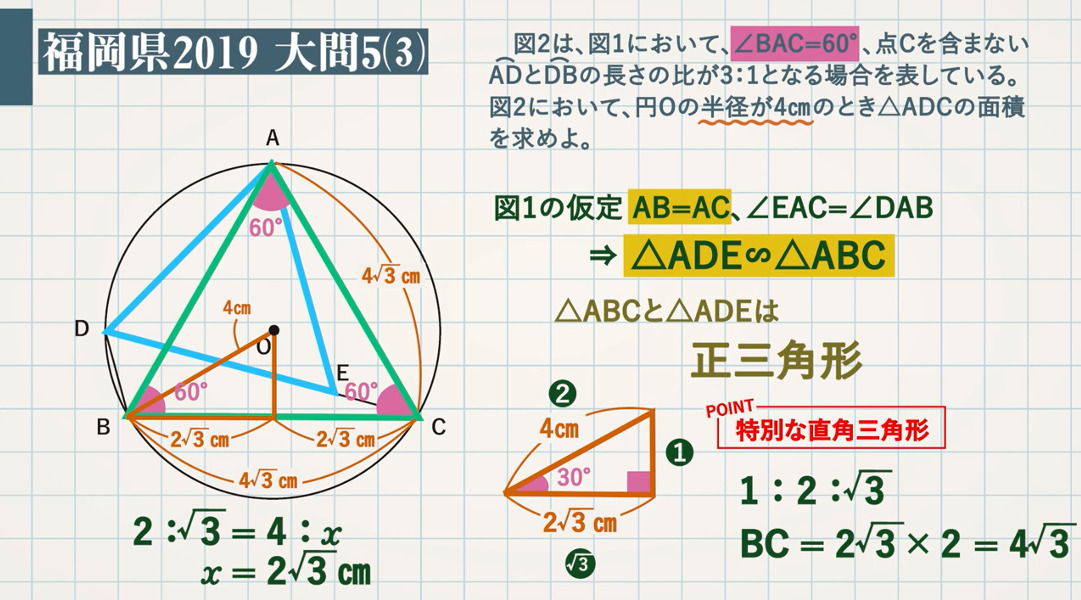



円周角 相似 三平方 特別な直角三角形の比を使い面積を求める 教遊者




中3数学 円周角の定理 の3大重要ポイント 映像授業のtry It トライイット
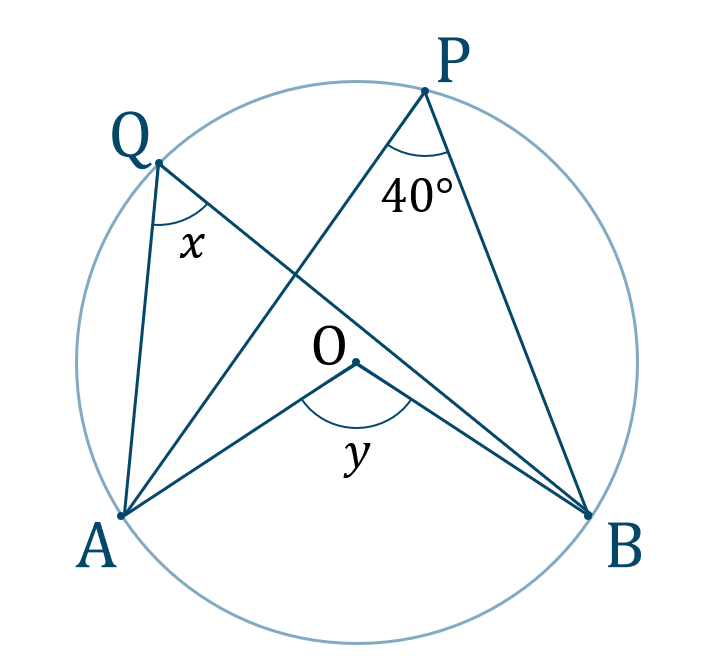



数学a 円周角と中心角の関係の使い方とコツ 教科書より詳しい高校数学
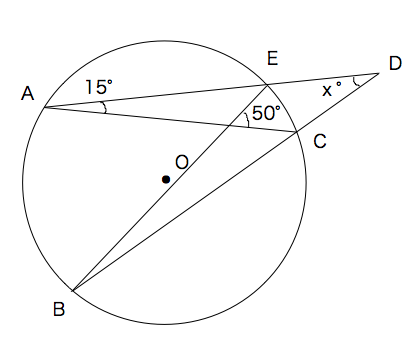



円周角の定理 練習問題 苦手な数学を簡単に
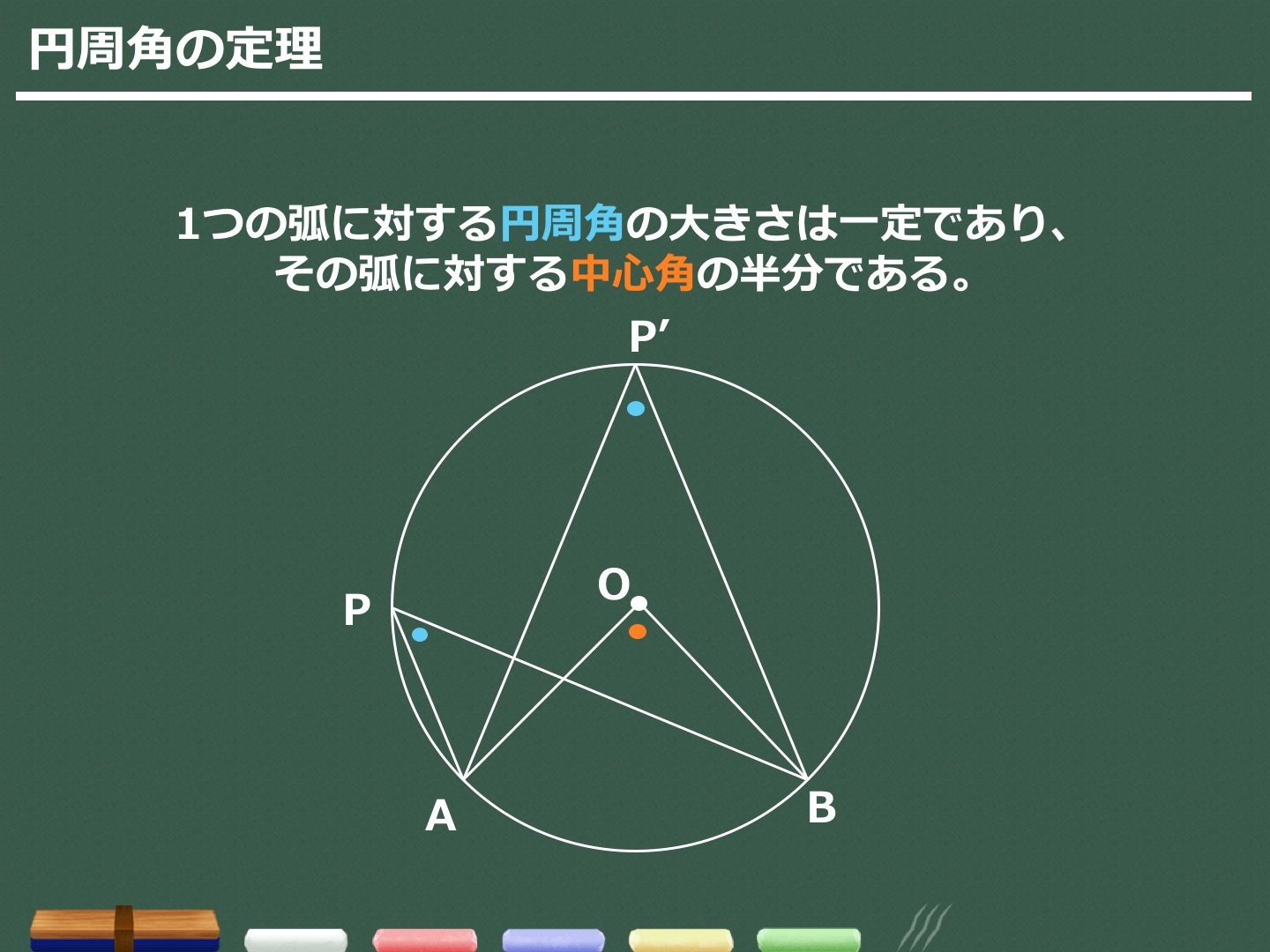



3分でわかる 円周角の定理とその逆の証明 問題の解き方 合格サプリ



円周角




円の性質 円周角の角度の求め方の3つのパターン Qikeru 学びを楽しくわかりやすく




中3数学 円の角度の求め方 練習編 映像授業のtry It トライイット




外接円の半径rを三角形の3辺からもとめる Schoolmath S Diary




円周角 Wikipedia
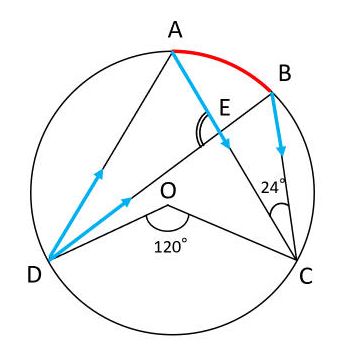



円周角の定理 円に内接する図形の角度を求める問題を攻略しよう みみずく戦略室
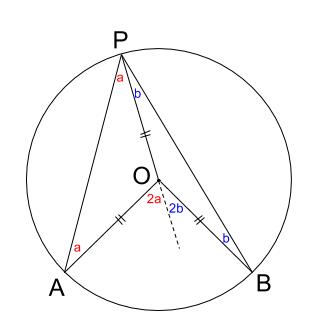



中学数学 円周角の定理はなぜ成り立つのか 中学数学の無料オンライン学習サイトchu Su




円の性質 円周角の角度の求め方の3つのパターン Qikeru 学びを楽しくわかりやすく




円周角の定理の逆 Youtube




数学 中3 57 円周角の定理 少し応用編 Youtube
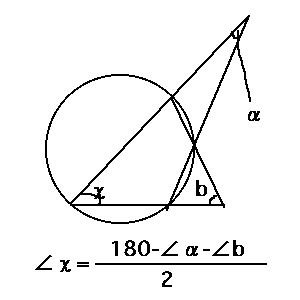



角度を求めよう 円とブーメラン 中学数学 Wiki Atwiki アットウィキ



同じ弧に対する円周角



円周角の定理 練習問題 角度がわからない 苦手な数学を簡単に




数学aの円で使う定理 性質の一覧 数学a By となりがトトロ マナペディア
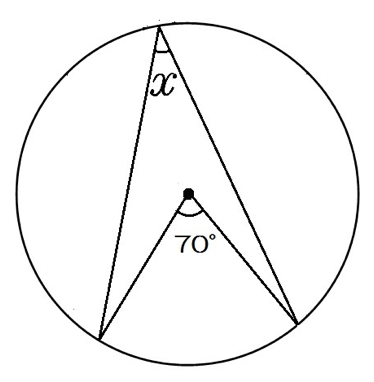



円の性質 円周角の角度の求め方の3つのパターン Qikeru 学びを楽しくわかりやすく
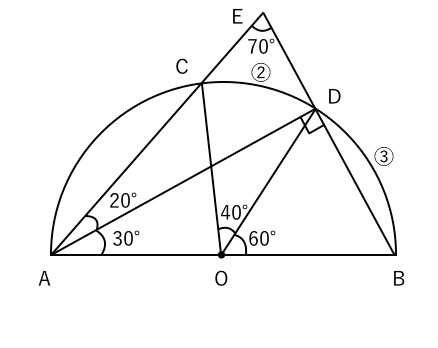



円周角と比の問題 苦手な数学を簡単に




数学aの円で使う定理 性質の一覧 数学a By となりがトトロ マナペディア




Mathematics 円 4 円周角の難しい問題を解くコツ 働きアリ



中3数学 パターン確認 円周角と相似 個別指導塾のyou 学舎日記 公式ブログ



数学 円周角の定理 岩手県公立高校入試問題




ファイル 円周角5 Jpg Wikibooks
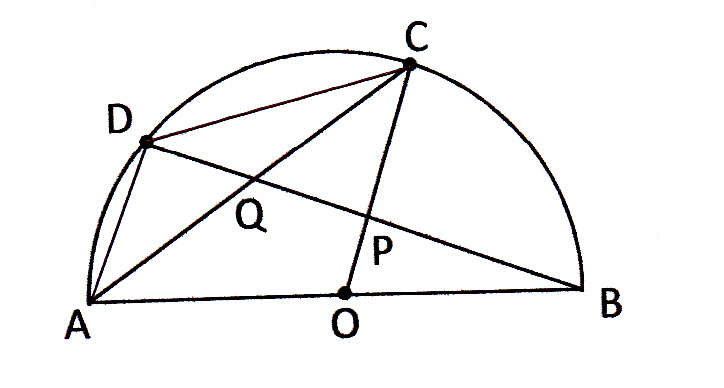



円周角の定理を使った相似の証明の解き方 現役塾講師のわかりやすい中学数学の解き方



中学数学 円周角の定理 例題その4 中学数学の無料オンライン学習サイトchu Su



円周角



図形の性質 円周角について 日々是鍛錬 ひびこれたんれん




数学 角の二等分線にまつわる絶対に覚えておきたい公式 受験の秒殺テク 8 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo



角度 直径と円周角 中学から数学だいすき




円周角の定理と角度を求める問題10選 中心角 ターレスの定理 内接する四角形 教遊者




円周角の定理 円に内接する四角形等図形の練習問題 中学 高校数学 身勝手な主張



毎日問題を解こう 7 苦手な数学を簡単に



円周角の定理とは 定理の逆や証明 問題の解き方 受験辞典




円周角の定理 円周角と中心角の関係は中学や高校でよく出るぞ 中学や高校の数学の計算問題



中学数学 円周角 中心角




円周角の定理の逆 無料で使える中学学習プリント




中3数学 円周角 ブーメラン型四角形 まとめと問題



円周角の定理とその逆の証明 高校数学マスター




中3数学 円周角の定理の逆 例題編 映像授業のtry It トライイット




接弦定理とは何か 角度別に分かるその証明方法 アタリマエ



中3数学 円周角の角度を求めるポイントと練習問題 デルココ



円周角の定理 Geogebra




円周角の定理 証明 逆をスマホで見やすい図で徹底解説 高校生向け受験応援メディア 受験のミカタ



中3数学 円周角の定理を使った定期テスト予想問題 Pikuu



中3数学 パターン確認 円周角と相似 個別指導塾のyou 学舎日記 公式ブログ



円と三角形 角度3 中学から数学だいすき




円周角の定理と角度を求める問題10選 中心角 ターレスの定理 内接する四角形 教遊者



円の中からはみ出ている三角形の問題はどう解けばいいですか 角度x角度yを Yahoo 知恵袋



角度 直径と円周角 中学から数学だいすき
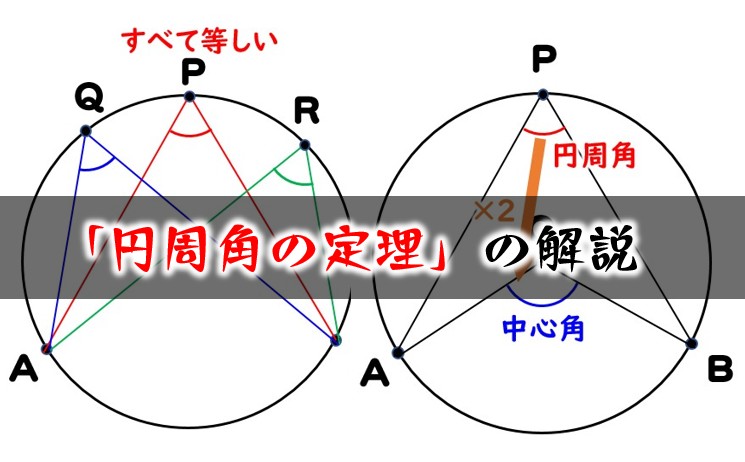



円周角の定理の解説 問題の解き方 数学fun
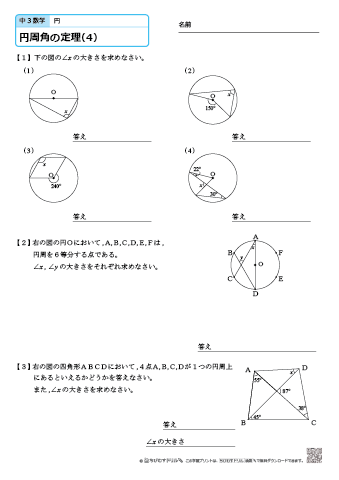



中学3年生 数学 円周角の定理 練習問題プリント ちびむすドリル 中学生




数学 中3 59 円周角の証明チャレンジ Lv 1 Youtube




中3数学 円周角 ブーメラン型四角形 まとめと問題
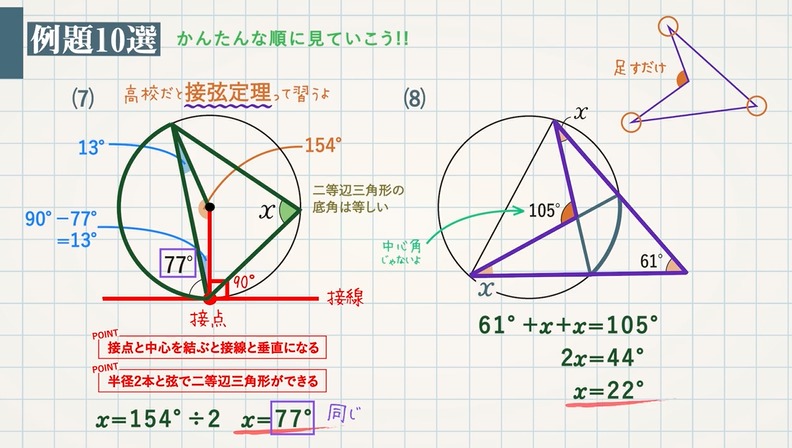



円周角の定理と角度を求める問題10選 中心角 ターレスの定理 内接する四角形 教遊者
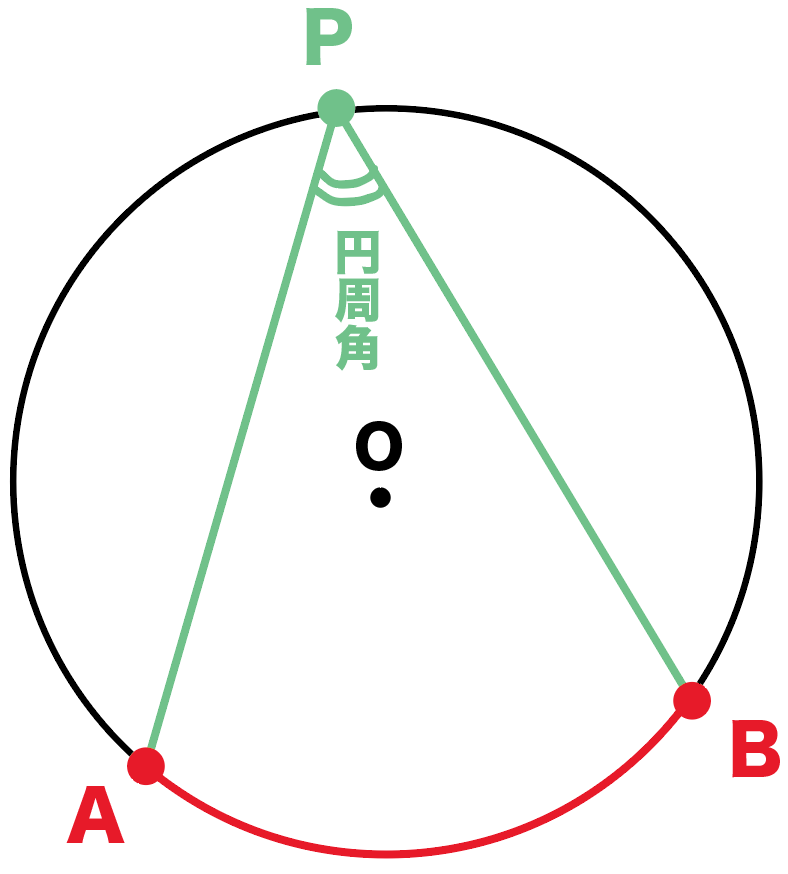



3分でわかる 円周角の定理とはなんだろう Qikeru 学びを楽しくわかりやすく




円周角の定理と角度を求める問題10選 中心角 ターレスの定理 内接する四角形 教遊者




中3数学 円周角の定理 の3大重要ポイント 映像授業のtry It トライイット




円周角の定理の基本 計算 無料で使える中学学習プリント
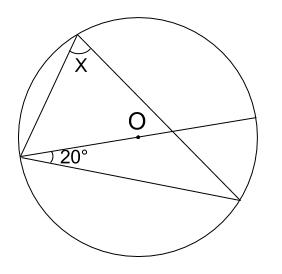



中学数学 円周角の定理 例題その3 中学数学の無料オンライン学習サイトchu Su



内接円 内心
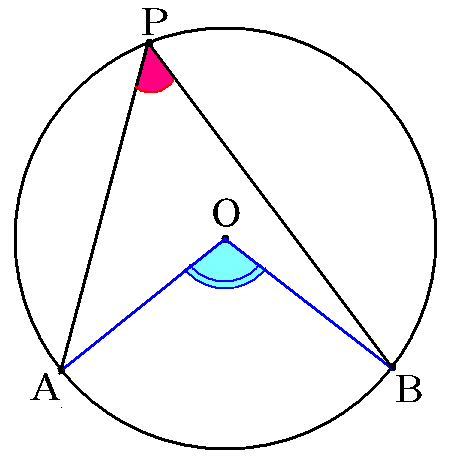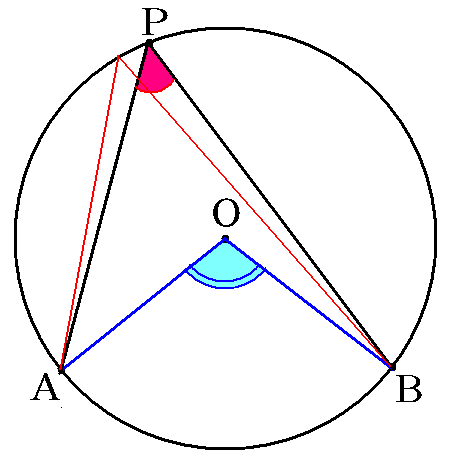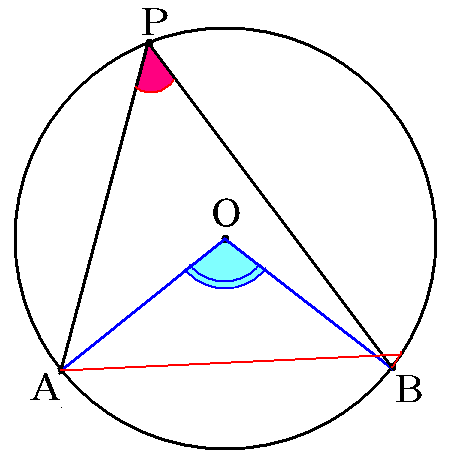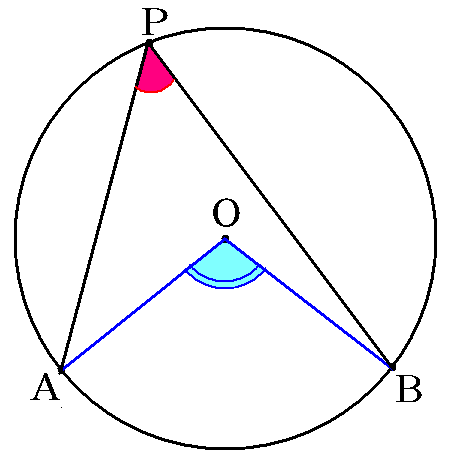



円周角の定理を表す動画 Takapの数学日記



余弦定理
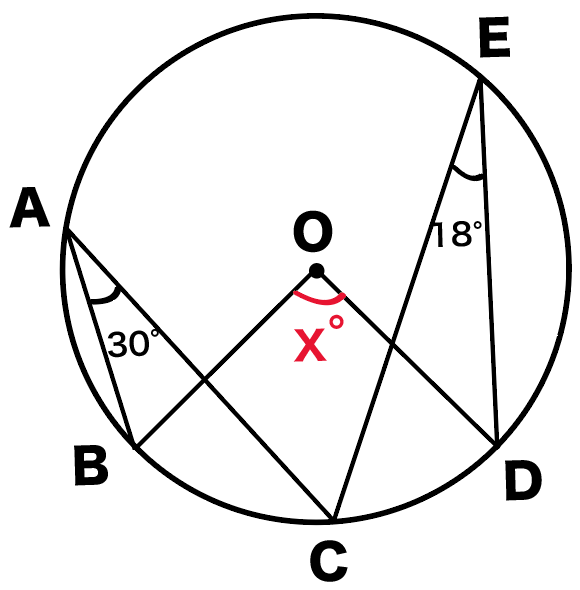



円周角の定理で角度を求める問題の解き方3ステップ Qikeru 学びを楽しくわかりやすく



円と三角形 角度 中学から数学だいすき




10月1日更新 半円を弧にする円周角についての証明 成績 上がってます 根城学習塾 八戸市
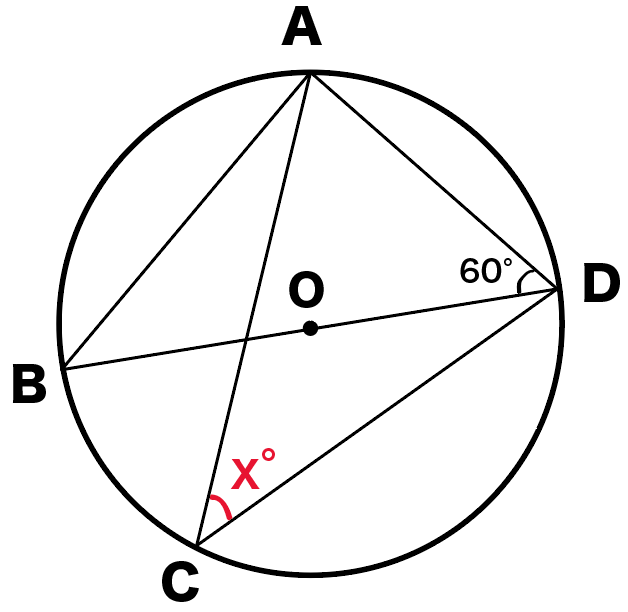



円周角の定理で角度を求める問題の解き方3ステップ Qikeru 学びを楽しくわかりやすく




円周角の定理 円の中にブーメラン型があるときの角度の求め方 数スタ
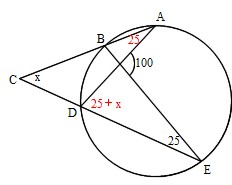



Mathematics 円 4 円周角の難しい問題を解くコツ 働きアリ

コメント
コメントを投稿